
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Непрерывные случайные величины
5. Равномерная случайная величина 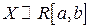 .
.
 Плотность вероятностей случайной величины
Плотность вероятностей случайной величины  , равномерно распределенной на отрезке
, равномерно распределенной на отрезке 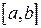 , имеет вид:
, имеет вид:
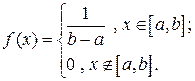
Найдем характеристическую функцию случайной величины 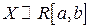 .
.
По определению характеристической функции непрерывной случайной величины (4.23) имеем:
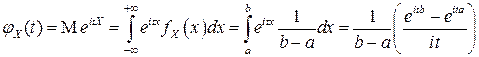 .
.
В частности:
если 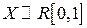 , то
, то
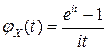 ;
;
если 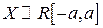 , то характеристическая функция является вещественной (см. свойство
, то характеристическая функция является вещественной (см. свойство 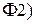 )
)
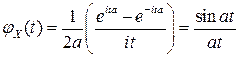 .
.
| Окончательно, | 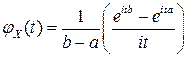 . .
|
6. Показательная (экспоненциальная) случайная величина 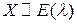 .
.
Плотность вероятностей показательно распределенной случайной величины  имеет вид:
имеет вид:
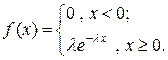
Найдем характеристическую функцию случайной величины 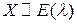 :
:
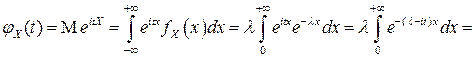
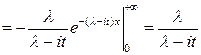 .
.
| Окончательно, | 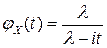 . .
|
7. Нормальная (гауссовская) случайная величина  .
.
 Плотность вероятностей нормально распределенной с параметрами
Плотность вероятностей нормально распределенной с параметрами 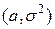 случайной величины
случайной величины  имеет вид:
имеет вид:
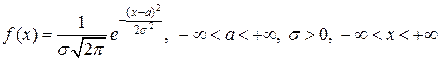 .
.
Найдем характеристическую функцию случайной величины  .
.
Известно, что случайную величину  можно получить с помощью линейного преобразования
можно получить с помощью линейного преобразования 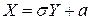 , где
, где 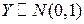 . Поэтому найдем вначале характеристическую функцию
. Поэтому найдем вначале характеристическую функцию 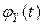 стандартной нормальной случайной величины
стандартной нормальной случайной величины 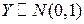 , а затем используем свойство
, а затем используем свойство 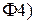 для нахождения
для нахождения 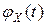 .
.
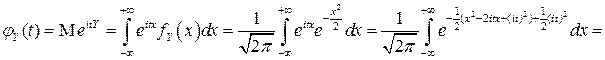
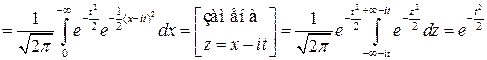 .
.
(при выкладках были использованы аналитичность подинтегральной функции на всей плоскости и интеграл Пуассона).
В соответствии со свойством 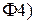 имеем:
имеем:
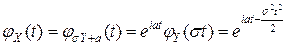 .
.
| Окончательно, | 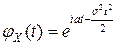 . .
|
Пример. Заданы две независимые нормальные случайные величины: 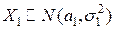 и
и 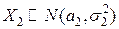 . Найти плотность вероятностей случайной величины
. Найти плотность вероятностей случайной величины 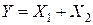 или, другими словами, найти композицию двух нормальных законов распределения.
или, другими словами, найти композицию двух нормальных законов распределения.
Решение. Известно, что характеристические функции случайных величин 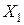 и
и 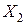 имеют вид:
имеют вид:
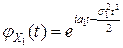 и
и 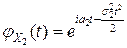 .
.
В соответствии со свойством 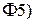 характеристическая функция случайной величины
характеристическая функция случайной величины 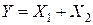 равна произведению характеристических функций слагаемых:
равна произведению характеристических функций слагаемых:
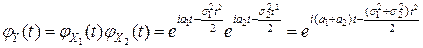 .
.
Но в силу теоремы единственности (следствие 3 из формулы обращения 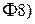 ) это означает, что случайная величина
) это означает, что случайная величина 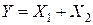 имеет также нормальный закон распределения:
имеет также нормальный закон распределения:  .
.
Замечание. Законы распределения, сохраняющиеся при линейных преобразованиях над случайными величинами, называются устойчивыми. Рассмотренный пример доказывает устойчивость нормального закона распределения. Устойчивыми также являются биномиальный и пуассоновский законы распределения (показать самостоятельно).
Задача. Используя характеристические функции, найти все центральные моменты 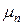 случайной величины
случайной величины  .
.
Замечание (о производящих функциях).
Пусть  - дискретная случайная величина, принимающая целые неотрицательные значения, закон распределения которой известен, то есть известно ее множество возможных значений
- дискретная случайная величина, принимающая целые неотрицательные значения, закон распределения которой известен, то есть известно ее множество возможных значений 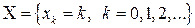 и вероятности значений
и вероятности значений 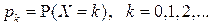 .
.
Производящей функцией целочисленной случайной величины  называется функция
называется функция 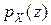 комплексной переменной
комплексной переменной 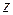 , определяемая при
, определяемая при 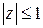 равенством
равенством
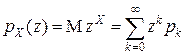 .
.
Производящая функция 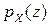 является аналитической внутри единичного круга
является аналитической внутри единичного круга 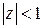 и по ней закон распределения целочисленной случайной величины X однозначно определяется равенствами:
и по ней закон распределения целочисленной случайной величины X однозначно определяется равенствами:
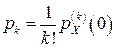 , где
, где 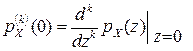 , k³0.
, k³0.
Так как 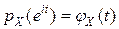 есть характеристическая функция целочисленной случайной величины
есть характеристическая функция целочисленной случайной величины  , то для производящих функций остаются справедливыми все свойства характеристических функций с теми лишь изменениями, которые вытекают из замены аргумента. Но использование на практике производящих функций при исследовании целочисленных случайных величин существенно проще, чем характеристических.
, то для производящих функций остаются справедливыми все свойства характеристических функций с теми лишь изменениями, которые вытекают из замены аргумента. Но использование на практике производящих функций при исследовании целочисленных случайных величин существенно проще, чем характеристических.
В частности (показать самостоятельно):
производящая функция 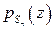 суммы
суммы 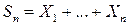 независимых целочисленных случайных величин равна произведению производящих функций слагаемых:
независимых целочисленных случайных величин равна произведению производящих функций слагаемых:
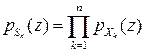 ;
;
моменты первых двух порядков целочисленной случайной величины  определяются через ее производящую функцию
определяются через ее производящую функцию 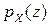 равенствами:
равенствами:
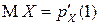 ,
, 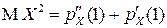 ,
, 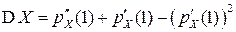 .
.
Задача 1. Найти производящие функции случайных величин 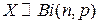 ,
, 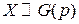 ,
, 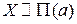 и по ним определить их числовые характеристики
и по ним определить их числовые характеристики 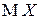 и
и 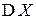 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Дискретные случайные величины | | | Характеристические функции случайных векторов |
Дата добавления: 2015-06-30; просмотров: 241; Нарушение авторских прав

Мы поможем в написании ваших работ!