Определение 22

Трехсторонник – это фигура, которая состоит из трех прямых, не проходящих через одну и ту же точку, и трех точек попарного их пересечения.

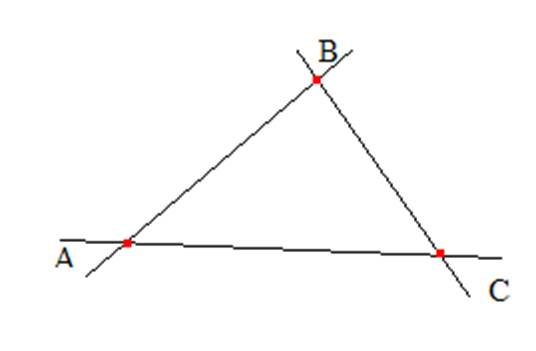
А,В,С – вершины, прямые АВ,ВС,АС – стороны.

Рассмотрим два трехвершинника АВСиА¢В¢С¢–фигуры, состоящие из трех точек, не лежащих на одной прямой, и трех прямых,.

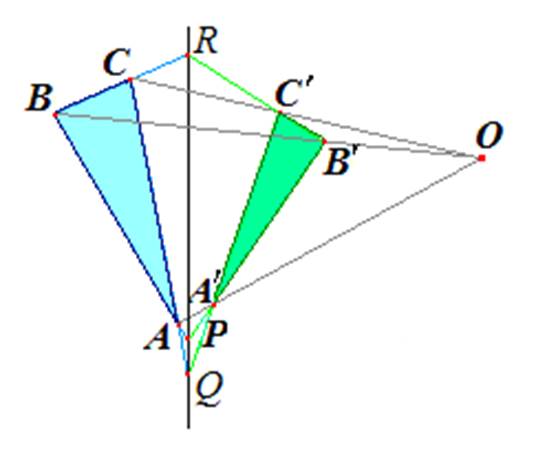
Теорема2 Дезарга

Если прямые, проходящие через соответствующие вершины двух трехвершинников, пересекаются в одной точке, то соответствующие стороны этих трехвершинников пересекаются в точках, лежащих на одной прямой.

Дано:

1) ABÇA'B'=Р,

2) ACÇA'C'=Q,

3) BCÇB'C'=R,

4) AA'ÇBB'ÇCC'=O.

Доказать: P,Q,R лежат на одной прямой.

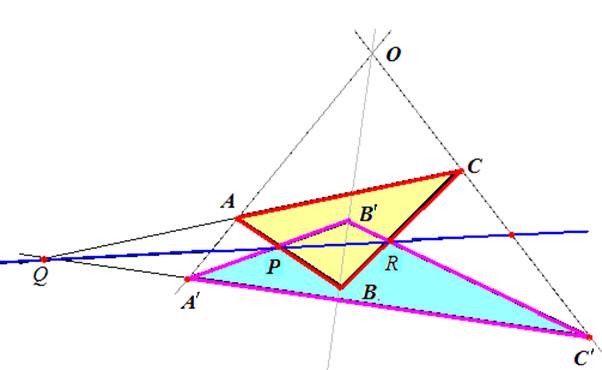
Доказательство

Надо показать, что векторы, порождающие точки P,Q,R линейно зависимы!

Рассмотрим векторы, порождающие соответствующие точки:

, , , , , , , , ,

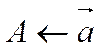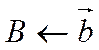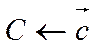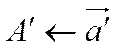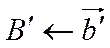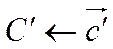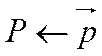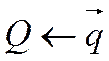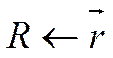Из (4) Точки А, А', О лежат на одной прямой, значит, векторы 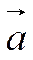и 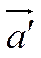, порождающие их, линейно зависимы, т.е.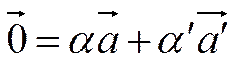

при .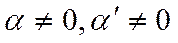

Аналогично, точки В', В, О лежат на одной прямой Þ ,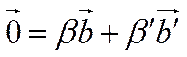

точки С, С', О лежат на одной прямой Þ .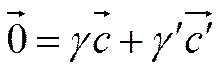

Получим

= =

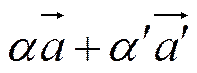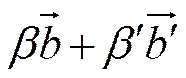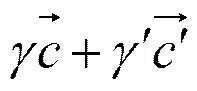
откуда получим равенства

= ,

= ,

= .

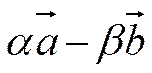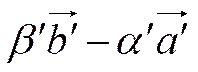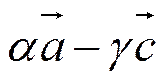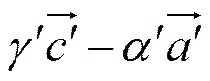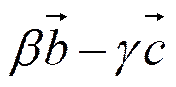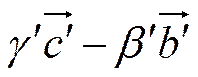Из (1) P=ABÇA'B',т.е. точки А,В,Р Î одной прямой. Значит, векторы 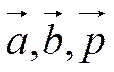– линейно зависимы,

|| ,

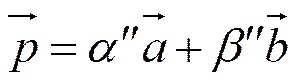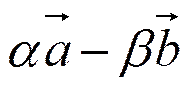т.е. можно выбрать

= = .

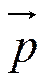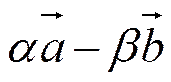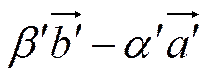Из (2) аналогично, так как Q=АСÇА'С', = = ,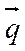

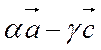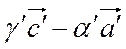Из (3) так как R=ВСÇВ'С', то = = .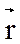

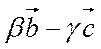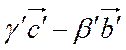Найдем сумму векторов .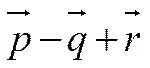

=( )–( )+( )= .

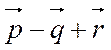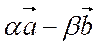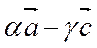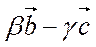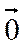или

=( )–( )+( )= .

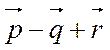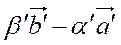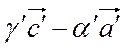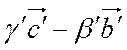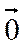Значит,

векторы 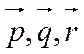линейно зависимы, а точки P,Q,R лежат на одной прямой.

Теорема доказана.

Дата добавления: 2015-06-30; просмотров: 296; Нарушение авторских прав

Мы поможем в написании ваших работ!