
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Сравнение множеств. Эквивалентные множества
Пусть A,B – два конечных множества. Если множество A состоит из 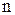 элементов, а множество B из
элементов, а множество B из 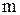 элементов, то между
элементов, то между 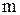 и
и 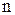 может существовать одно из соотношений:
может существовать одно из соотношений: 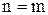 ,
, 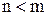 ,
, 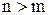 . Какое из этих соотношений действительно имеет место легко установить.
. Какое из этих соотношений действительно имеет место легко установить.
Если множества бесконечны, то говорить о количестве элементов не имеет смысла, а значит и сравнивать эти множества по количеству элементов нельзя. В этом случае используется метод установления взаимно однозначного соответствия.
Определение.Если каждому элементу 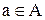 поставлен в соответствие один и только один элемент
поставлен в соответствие один и только один элемент 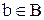 и наоборот, то между элементами множеств A и B установлено взаимно однозначное соответствие.
и наоборот, то между элементами множеств A и B установлено взаимно однозначное соответствие.
Определение.Если между элементами двух различных множеств A и B установлено взаимно однозначное соответствие, то эти множества называются эквивалентными и записываются так: 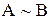 .
.
Из определения эквивалентности множеств следуют следующие свойства:
· 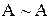 (рефлексивность);
(рефлексивность);
· если 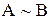 , то
, то 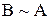 (симметричность);
(симметричность);
· если 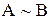 и
и 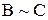 , то
, то 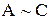 (транзитивность).
(транзитивность).
Пример. Множество натуральных чисел N эквивалентно множеству четных натуральных чисел, т.к. каждому 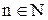 ставим в соответствие
ставим в соответствие 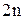 (четные числа). Кроме того, множество
(четные числа). Кроме того, множество 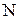 эквивалентно множеству нечетных натуральных чисел т.к. каждому
эквивалентно множеству нечетных натуральных чисел т.к. каждому 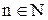 можно поставить в соответствие нечетное натуральных число
можно поставить в соответствие нечетное натуральных число 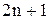 .
.
Введем следующие обозначения:
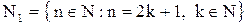 – множество нечетных натуральных чисел;
– множество нечетных натуральных чисел;
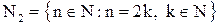 – множество четных натуральных чисел.
– множество четных натуральных чисел.
Тогда 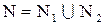 , причем
, причем 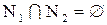 и
и 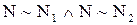 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Задание признаком | | | Подмножества множеств. Алгебра подмножеств |
Дата добавления: 2015-06-30; просмотров: 239; Нарушение авторских прав

Мы поможем в написании ваших работ!