Подмножества множеств. Алгебра подмножеств

Два множества A и B равны, если они состоят из одних и тех же элементов.

Из этого принципа следует, что для любых двух различных множеств всегда найдется некоторый объект, являющийся элементом одного из них и не являющийся элементом другого. Так как пустые совокупности не содержат элементов, то они не различимы и поэтому пустое множество – единственно.

Подмножества.Определение равенства множеств можно сформулировать иначе, используя понятие подмножества.

Определение. Множество A называется подмножеством множества B 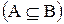, если каждый элемент A является элементом B.

.

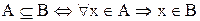Следствие 1. Очевидно, для любого множества A, т.к. каждый элемент из A есть элемент из A.

Следствие 2. Для любого множества A, 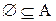, ибо если бы пустое множество не являлось подмножеством A, то в пустом подмножестве существовали бы элементы, не принадлежащие A. Однако пустое множество не содержит вообще ни одного элемента.

Если 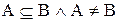, то пишут 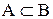, и если 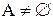, то A – собственное подмножество B.

Понятие подмножества множеств позволяет легко формализовать понятие равенства двух множеств.

Утверждение.Для любых A и B

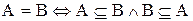. (1.1)

Логическую эквивалентность, определяемую выражением (1.1) используют как основной способ доказательства равенства двух множеств.

Замечание.Отношение включения Í обладает рядом очевидных свойств:

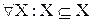(рефлексивность);

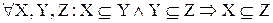(транзитивность).

Для любого множества X можно определить специальное множество всех подмножеств множества X, которое называется булеаном ℬ 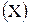, которое включает в себя само множество X, все его подмножества и пустое множество .

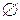Пример.Пусть 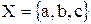– это множество, состоящее из трех элементов. Тогда булеан ℬ(X) это множество:

ℬ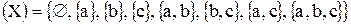

Собственными подмножествами ℬ(X) являются следующие множества:

{a},{b},{c},{a,b},{b,c},{a,c}.

В общем случае, если множество X содержит n элементов, то множество его подмножеств ℬ(X) состоит из 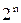элементов.

Дата добавления: 2015-06-30; просмотров: 264; Нарушение авторских прав

Мы поможем в написании ваших работ!