Операции на множествах

Пусть U – универсальное множество, 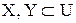. Тогда для множеств X,Y можно определить операции .

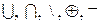Определение.Объединением множеств X и Y называется множество 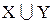, состоящее из элементов, входящих хотя бы в одно из множеств (X или Y):

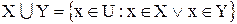. (1.2)

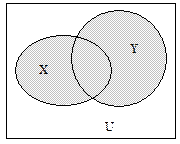
Рис. 1.1 – Объединение множеств Рис. 1.2 – Пересечение множеств

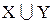
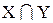
Определение. Пересечением множеств X и Y называется множество 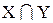, состоящее из элементов, входящих в X и в Y одновременно:

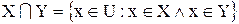. (1.3)

Определение. Разностью множеств X и Y называется множество 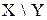, состоящее из элементов, входящих в множество X, но не входящих в Y:

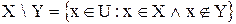. (1.4)

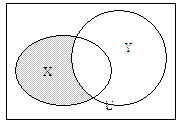
Рис. 1.3 – Разность множеств 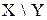Рис. 1.4 – Симметрическая

разность множеств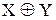

Определение. Симметрической разностью двух множеств X и Y называется множество 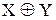, состоящее из элементов множества X и элементов множества Y, за исключением элементов, являющихся общими для обоих множеств:

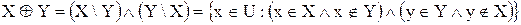. (1.5)

Определение. Для любого множества 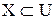дополнением множества 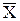до U называется такое множество 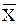, что:

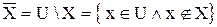. (1.6)

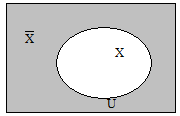
Рис. 1.5 – Дополнение 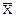множества X до U

На рис. 1.1 ¸ 1.5 представлены диаграммы Венна, наглядно демонстрирующие результаты операций .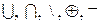

Дополнение множества иногда обозначается 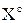. Операции 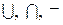связаны между собой законами де Моргана:

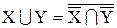, (1.7)

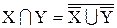. (1.8)

В справедливости законов де Моргана легко убедиться самостоятельно.

В таблице 1.1 представлены основные свойства операций над множествами.

Таблица 1.1

№	Свойства операций	Объединение, пересечение, дополнение
	коммутативность	,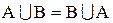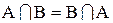
	ассоциативность	,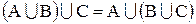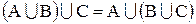
	дистрибутивность	,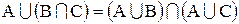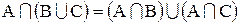
	идемпотентность	, , , , ,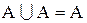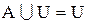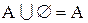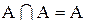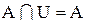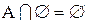
	теоремы де Моргана	,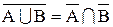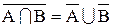
	инволюция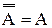

Операции объединения и пересечения можно обобщить. Пусть 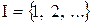– множество индексов, 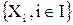– семейство подмножеств множества X.

Определение. Семейство подмножеств 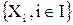множества X, для которых 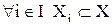, называется разбиением множества X, если выполняются следующие два условия:

,

.

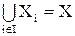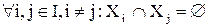Определение.Семейство подмножеств 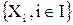множества X называется покрытием множества X, если: .

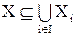Будем, как и ранее, считать, что все рассматриваемые множества являются подмножествами некоторого универсального множества U. Тогда имеет место следующее определение.

Определение. Класс K подмножеств из U называется алгеброй, если:

1. ;

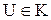2. из того, что 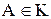следует, что ;

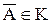3. из того, что 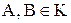следует, что .

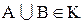Пример. Пусть 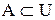, тогда класс 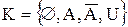образует алгебру.

Определение.Класс F подмножеств из U образует 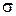-алгебру, если:

1. ;

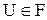2. из того, что 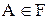следует ;

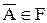3. из того, что 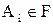, 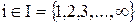следует, что .

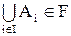Пример. Множество всех подмножеств U образует 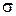-алгебру, т.е. ℬ(U) – 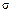-алгебра.

Дата добавления: 2015-06-30; просмотров: 247; Нарушение авторских прав

Мы поможем в написании ваших работ!