Мощность множества. Кардинальные числа

Рассмотрим множество A и совокупность всех множеств, эквивалентных множеству A. На основании свойства транзитивности все эти множества будут эквивалентны между собой.

Назовем такую совокупность множеств классом эквивалентности.

Каждому классу эквивалентности поставим в соответствие некоторый символ a (альфа), который будем называть кардинальным числом или мощностью каждого множества, входящего в данный класс эквивалентности.

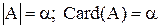. (1.9)

Таким образом, под мощностью множества 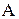понимается то общее, что присуще всем эквивалентным между собой множествам.

Если задан класс эквивалентных множеств 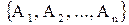и этому классу множеств поставлено в соответствие кардинальное числ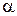о , то , , …, .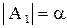

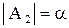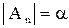Замечание.

1. Для конечных множеств понятие «число элементов» и понятие мощности множеств совпадают между собой.

2. Для бесконечных множеств понятие «число элементов» смысла не имеет. Можно говорить только о мощности множества. Понятие мощности есть естественное обобщение понятия числа элементов.

Пусть 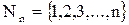– множество натуральных чисел меньших или равных .

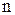Определение.Конечным множеством называется множество, равномощное множеству 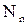– натуральных чисел меньших или равных 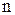. Оно содержит 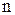элементов и его мощность равна 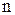. Пишут .

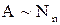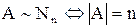. (1.10)

Мощность пустого множества равна нулю .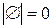

Определение.Непустое и неконечное множество называется бесконечным.

Теорема. Мощность множества A всегда строго меньше мощности множества всех его подмножеств.

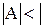ℬ 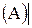. (1.11)

Следствие. Если

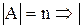ℬ 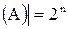. (1.12)

Определение. Всякое подмножество равномощное множеству натуральных чисел называется счетным, и его мощность равна 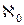(алеф нуль):

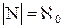. (1.13)

Замечание. Алеф – первая буква еврейского алфавита, а 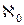– наименьшая мощность бесконечного множества.

Теорема. Множество всех подмножеств ℬ 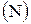множества натуральных чисел несчетно. Его мощность называется мощностью континуума и равна À₁ (алеф один):

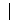ℬ 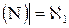. (1.14)

Пример.Мощность множества действительных чисел сегмента 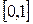равна мощности континуума.

Теорема.Всякое бесконечное множество содержит счетное подмножество.

Доказательство. Пусть A – бесконечное множество. Т.к. 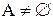, мы можем выбрать среди его элементов какой-нибудь один; пусть это будет 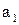, тогда множество 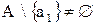; выберем в нем какой-либо другой элемент – например, 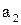. После выделения таким способом 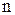элементов множество 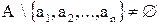, и можно выбрать еще один элемент, например, 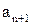и т.д. Следовательно, множество A содержит счетное подмножество .

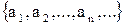Континуум-гипотеза:

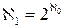. (1.15)

Теорема. Объединение множества континуума и конечного или счетного множества имеет мощность континуума.

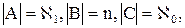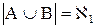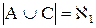Пусть тогда

, , а 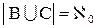. (1.16)

Теорема. Объединение конечного или счетного числа множеств мощности континуума имеет мощность континуума.

Дата добавления: 2015-06-30; просмотров: 322; Нарушение авторских прав

Мы поможем в написании ваших работ!