Формула

Задание. Найти производную функции

Решение. Искомая производная

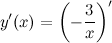
Константу - 3 выносим за знак производной (согласно правилам дифференцирования):

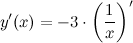
Тогда, согласно формуле получаем:

Или после упрощения

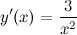
Ответ.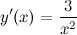

Если независимая переменная и функция связаны уравнением вида , которое не разрешено относительно , то функция называется неявной функцией переменной .

Предположим, что функциональная зависимость от не задана непосредственно , а через промежуточную величину — 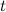. Тогда формулы

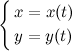
задают параметрическое представление функции одной переменной.

Геометрический смысл

Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

ЭЛАСТИЧНОСТЬ ФУНКЦИИ [function elasticity] (иногда ее называют относительной производной) — предел отношения относительного приращения функции y(зависимой переменной) к относительному приращению независимой переменной x когда Δx и Δy→ 0 обозначается символом E_x(y) и выражается следующей формулой:

Дифференцируемость функции в точке

2.Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества. Дифференцируемость является одним из фундаментальных понятий в математике и имеет значительное число приложений как в самойматематике, так и в других естественных науках.

Дифференциал - (от лат. differentia — разность, различие) — линейная частьприращения функции.

· Свойства
Матрица линейного оператора равна матрице Якоби; её элементами являются частные производные .

· Отметим, что матрица Якоби может быть определена в точке, где дифференциал не определён.

· Дифференциал функции связан с её градиентом 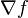следующим определяющим соотношением

Дата добавления: 2015-07-26; просмотров: 313; Нарушение авторских прав

Мы поможем в написании ваших работ!