
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Максимум и минимум функции
В таком случае, точку х = 0 называют точкой максимума функции. По аналогии с этим, точку х = 2 называют точкой минимума функции y = x^3 – 3*x^2. Потому что существует такая окрестность этой точки, в которой значение в этой точке будет минимальным среди всех других значений из этой окрестности.
Точкой максимума функции f(x) называется точка x0, при условии, что существует окрестность точки х0 такая, что для всех х не равных х0 из этой окрестности, выполняется неравенство f(x) < f(x0).
Точкой минимума функции f(x) называется точка x0, при условии, что существует окрестность точки х0 такая, что для всех х не равных х0 из этой окрестности, выполняется неравенство f(x) > f(x0).
В точках максимума и минимума функций значение производной функции равно нулю. Но это не достаточное условие для существования в точке максимума или минимума функции.
Например, функция y = x^3 в точке х = 0 имеет производную равную нулю. Но точка х = 0 не является точкой минимума или максимума функции. Как известно функция y = x^3 возрастает на всей числовой оси.
Таким образом, точки минимума и максимума всегда будут находиться среди корне уравнения f’(x) = 0. Но не все корни этого уравнения будут являться точками максимума или минимума.
Исследование функции на монотонность
Теорема 1. Если во всех точках открытого промежутка X выполняется неравенство f′(x)≥0 (причем равенство f′(x)=0 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке) , то функция y=f(x)) возрастает на промежутке X.
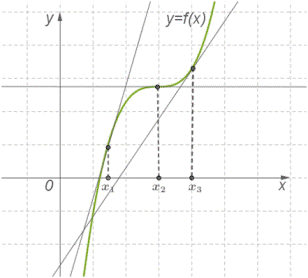
Теорема 2. Если во всех точках открытого промежутка X выполняется неравенство f′(x)≤0 (причем равенство f′(x)=0 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция y=f(x) убывает на промежутке X.
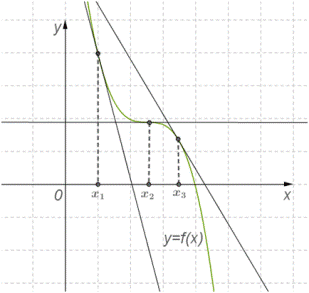
Итак:
если существует производная функции в интервале (a,b) и в данном интервале
1) f'(x)≥0, то функция в нём не убывает;
2) f'(x)≤0, то функция в нём не возрастает;
3) f'(x)>0, то функция в нём возрастает;
4) f'(x)<0, то функция в нём убывает.
Пример:
Необходимо исследовать интервалы монотонности функции f(x)=x3−4x2−16x+17.
Сначала находим производную: f'(x)=(x3−4x2−16x+17)'=3x2−8x−16.
Это парабола, которая пересекает ось x в точках x1=−43 и x2=4 и чьи ветви направлены вверх. Поэтому производная отрицательна в интервале (−43;4) (функция убывает) и положительна в интервалах (−∞;−43) и (4;+∞) (функция возрастает).
Ответ:
функция f(x)=x3−4x2−16x+17 возрастает в интервалах (−∞;−43) и (4;+∞), убывает в интервале (−43;4).
Выпуклость графика функции
График функции  , дифференцируемой на интервале
, дифференцируемой на интервале  , является на этом интервале выпуклым, если график этой функции в пределах интервала
, является на этом интервале выпуклым, если график этой функции в пределах интервала  лежит не выше любой своей касательной
лежит не выше любой своей касательной
Точкой перегиба графика функции  называется точка
называется точка  , разделяющая промежутки выпуклости и вогнутости.
, разделяющая промежутки выпуклости и вогнутости.
Схема нахождения промежутков выпуклости и точек перегиба графика
Асимптоты графика функции (вертикальные и наклонные)
Асимптота – этопрямая, к которой неограниченно близко приближается график функции при удалении его переменной точки в бесконечность.
1) Вертикальные асимптоты, которые задаются уравнением вида  , где «альфа» – действительное число. Популярная представительница
, где «альфа» – действительное число. Популярная представительница  определяет саму ось ординат, вспоминаем гиперболу
определяет саму ось ординат, вспоминаем гиперболу  .
.
Вертикальная асимптота графика, как правило, находится в точке бесконечного разрывафункции. Всё просто: если в точке  функция
функция  терпит бесконечный разрыв, то прямая, заданная уравнением
терпит бесконечный разрыв, то прямая, заданная уравнением  является вертикальной асимптотой графика.
является вертикальной асимптотой графика.
2) Наклонные асимптоты традиционно записываются уравнением прямой с угловым коэффициентом 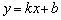 . Иногда отдельной группой выделяют частный случай –горизонтальные асимптоты
. Иногда отдельной группой выделяют частный случай –горизонтальные асимптоты 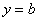 . Например, та же гипербола с асимптотой
. Например, та же гипербола с асимптотой  .
.
Наклонные (как частный случай – горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше 2-х наклонных асимптот. Например, график экспоненциальной функции  обладает единственной горизонтальной асимптотой при
обладает единственной горизонтальной асимптотой при  , а график арктангенса
, а график арктангенса  при
при  – двумя такими асимптотами, причём различными.
– двумя такими асимптотами, причём различными.
Функции несколько переменных и их непрерывность
1.Основные понятия.
Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.
Обычно функция нескольких переменных задается явным аналитическим способом. Например: z=3x+5y2,u=xy+z2 и т.д.
Встречается также и неявное задание таких функций, например: z-2x-sinxy=0.
Упорядоченная пара чисел (x,y) может рассматриваться как точка на плоскости, т.е. Z есть функция точки (x,y).
Чтобы задать функцию z=f(x,y), надо не только указать правило нахождения z по заданным xи y, но и то множество (называемое областью задания функции) пар значений, которые могут принимать аргументы x и y.
Например, функция z= 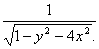 задана только при 1-y
задана только при 1-y  >0, т.е. внутри эллипса y2+4x2<1 с полуосями, а=0,5 и в=1 не включая точки, лежащие на эллипсе.
>0, т.е. внутри эллипса y2+4x2<1 с полуосями, а=0,5 и в=1 не включая точки, лежащие на эллипсе.



 Определение. Если каждой совокупности значений переменных x,y,z…tсоответствует определенное значение переменной w, то wназывается функцией независимых переменных x,y,z…t и записывается w=f(x,y,z…t).
Определение. Если каждой совокупности значений переменных x,y,z…tсоответствует определенное значение переменной w, то wназывается функцией независимых переменных x,y,z…t и записывается w=f(x,y,z…t).
Для функции трех переменных областью определения является упорядоченная тройка чисел (x,y,z), т.е. некоторая совокупность точек пространства. Область определения функции четырех и большего числа переменных не допускает простого геометрического истолкования. 
Функции двух переменных допускают графическую иллюстрацию. Графиком функцииz=f(x,y), заданной на некотором множестве D точек плоскости ХОУ, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежит D, а z=f(x,y). В наиболее простых случаях такой график представляет собой некоторую поверхность.
Например, графиком функции z=4-x2-y2 является параболоид.
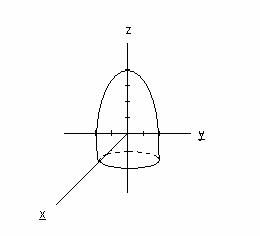
Функции трех и большего числа переменных не имеют геометрического представления.
2.Непрерывность функции нескольких переменных.
Определение. Число А называется пределом функцииf(M), где М(x1,x2,…xn) – точка n-мерного пространства, при стремлении точки М к точке М0(x10,x20,…xn0) любым образом, если для всякого сколь угодно малого  >0 существует такое число
>0 существует такое число  >0, что из условия
>0, что из условия 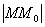 <
<  , где
, где 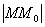 - расстояние между точкамиМ и М0, следует
- расстояние между точкамиМ и М0, следует  <
<  .
.
Обозначается:
А  .
.
Пусть z=f(x,y). Придадим x и y приращения  и
и 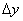 . Получим приращение
. Получим приращение  функцииz=f(x,y). Если
функцииz=f(x,y). Если
 , (1)
, (1)
т.е. бесконечно малым аргументам соответствует бесконечно малое приращение функции, то говорят, что функция непрерывна.
Распишем  x0+
x0+  y+
y+  -f(x0,y0) и положим x0+
-f(x0,y0) и положим x0+  x=x,y0+
x=x,y0+  ,то выражение(1) можно записать в виде
,то выражение(1) можно записать в виде
 f(x,y)=f(x 0,y0), (2)
f(x,y)=f(x 0,y0), (2)
т.е. непрерывность функции означает, что ее предел равен ее значению от пределов аргументов.
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области. Если в некоторой точке не выполняется условие (2), то эта точка называется точкой разрыва.
| Производные и дифференциалы функции нескольких переменных |
Частной производной от функции  по независимой переменной по независимой переменной  называется производная называется производная
 , вычисленная при постоянном , вычисленная при постоянном 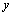 .
Частной производной по y называется производная .
Частной производной по y называется производная  , вычисленная при постоянном , вычисленная при постоянном  . Для частных производных справедливы обычные правила и формулы дифференцирования.
Пример 1. . Для частных производных справедливы обычные правила и формулы дифференцирования.
Пример 1.  .
Рассматривая .
Рассматривая 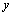 как постоянную величину как постоянную величину  , получим , получим  .
Рассматривая .
Рассматривая  как постоянную величину как постоянную величину  , получим , получим  .
Пример 2. .
Пример 2. 
 ; ; 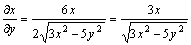 ; ;
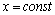 ; ;  .
Полным приращением функции .
Полным приращением функции  в точке в точке 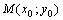 называется разность называется разность  , где , где  и и  произвольные приращения аргументов. Функция произвольные приращения аргументов. Функция  называется дифференцируемой в точке называется дифференцируемой в точке  , если в этой точке полное приращение можно представить в виде , если в этой точке полное приращение можно представить в виде  , где , где  .
Полным дифференциалом функции .
Полным дифференциалом функции  называется главная часть полного приращения называется главная часть полного приращения  , линейная относительно приращений аргументов , линейная относительно приращений аргументов  и и  , то есть , то есть 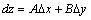 .
Полный дифференциал функции .
Полный дифференциал функции  вычисляется по формуле вычисляется по формуле  .
Для функции трех переменных .
Для функции трех переменных  .
При достаточно малом .
При достаточно малом  для дифференцируемой функции для дифференцируемой функции  справедливы приближенные равенства справедливы приближенные равенства  ; ; 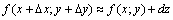 , которые применяются для приближенного вычисления значения функции , которые применяются для приближенного вычисления значения функции
 . (*)
Пример 3. Вычислить приближенное значение: . (*)
Пример 3. Вычислить приближенное значение:  .
Решение. Полагая, что .
Решение. Полагая, что  есть частное значение функции есть частное значение функции  в точке в точке  и что вспомогательная точка будет и что вспомогательная точка будет 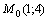 , получим , получим 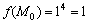
 ; ;  ; ; 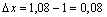 ; ;  .
Подставляя в формулу (*), найдем: .
Подставляя в формулу (*), найдем:
 .
Частными производными второго порядка от функции .
Частными производными второго порядка от функции  называются частные производные от ее частных производных первого порядка.
Обозначения частных производных второго порядка: называются частные производные от ее частных производных первого порядка.
Обозначения частных производных второго порядка:
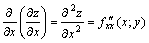 ; ;  ; ;
 ; ;  .
Смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они непрерывны: .
Смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они непрерывны: 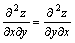 .
Дифференциалом второго порядка от функции .
Дифференциалом второго порядка от функции  называется дифференциал от ее полного дифференциала, то есть называется дифференциал от ее полного дифференциала, то есть  . Если . Если  и и 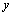 – независимые переменные и функция – независимые переменные и функция  имеет непрерывные производные, то дифференциал второго порядка вычисляется по формуле имеет непрерывные производные, то дифференциал второго порядка вычисляется по формуле 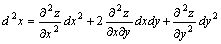 .
Пример 4. .
Пример 4.  . Найти . Найти 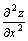 , , 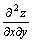 , ,  .
Решение. Найдем частные производные: .
Решение. Найдем частные производные:  ; ; 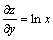 . Дифференцируя повторно, получим . Дифференцируя повторно, получим  ; ;
 ; ;  . .
|
Дата добавления: 2015-07-26; просмотров: 397; Нарушение авторских прав

Мы поможем в написании ваших работ!