Регулярные выражения и языки

Регулярные выражения являются достаточно удобным средством для построения "алгебраических" описаний языков. Они строятся из элементарных выражений с помощью операций объединения ( + ), конкатенации ( ) и итерации ( ^* ). Каждому такому выражению r соответствует представляемый им язык L_r. Смысл операции объединения языков мы знаем. Определим операции конкатенации и итерации (иногда ее называют замыканием Клини).

Пусть L₁ и L₂ - языки в алфавите

Тогда , т.е. конкатенация языков состоит из конкатенаций всех слов первого языка со всеми словами второго языка. В частности, если , то , а если , то .

Введем обозначения для "степеней" языка L:

Таким образом в Lⁱ входят все слова, которые можно разбить на i подряд идущих слов из L.

Итерацию (L)^* языка L образуют все слова которые можно разбить на несколько подряд идущих слов из L:

Ее можно представить с помощью степеней:

Часто удобно рассматривать "усеченную" итерацию языка, которая не содержит пустое слово, если его нет в языке: . Это не новая операция, а просто удобное сокращение для выражения .

Отметим также, что если рассматривать алфавит как конечный язык, состоящий из однобуквенных слов, то введенное ранее обозначение для множества всех слов, включая и пустое, в алфавите соответствует определению итерации этого языка.

В следующей таблице приведено формальное индуктивное определение регулярных выражений над алфавитом и представляемых ими языков.

Выражение r	Язык Lr
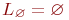
	La={a}
Пусть r1 и r2 -это	Lr1 и Lr2 -представляемые
регулярные выражения.	ими языки.
Тогда следующие выражения
являются регулярными	и представляют языки:
r=(r1+r2)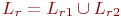
r=(r1circr2)
r=(r1)*	Lr=Lr1*

При записи регулярных выражений будем опускать знак конкатенации и будем считать, что операция ^* имеет больший приоритет, чем конкатенация и +, а конкатенация - больший приоритет, чем +. Это позволит опустить многие скобки. Например, 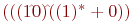можно записать как 10(1^* + 0).

Определение 5.1. Два регулярных выражения r и p называются эквивалентными, если совпадают представляемые ими языки, т.е. L_r=L_p. В этом случае пишем r = p.

Нетрудно проверить, например, такие свойства регулярных операций:

• r + p= p+ r (коммутативность объединения),
• (r+p) +q = r + (p+q) (ассоциативность объединения),
• (r p) q = r (p q) (ассоциативность конкатенации),
• (r^*)^* = r^* (идемпотентность итерации ),
• (r +p) q = rq + pq (дистрибутивность).

Пример 5.1. Докажем в качестве примера не столь очевидное равенство: (r + p)^* = (r^*p^*)^*.

Пусть L₁ - язык, представляемый его левой частью, а L₂ - правой. Пустое слово принадлежит обоим языкам. Если непустое слово , то по определению итерации оно представимо как конкатенация подслов, принадлежащих языку . Но этот язык является подмножеством языка L'=L_r^*L_p^* (почему?). Поэтому 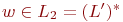. Обратно, если слово , то оно представимо как конкатенация подслов, принадлежащих языку L'. Каждое из таких подслов v представимо в виде v= v₁¹... v_k¹ v₁²... v_l², где для всех i=1, ... , k подслово 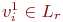и для всех j=1, ... , l подслово (возможно, что k или l равно 0). Но это значит, что w является конкатенацией подслов, каждое из которых принадлежит и, следовательно, .

Рассмотрим несколько примеров регулярных выражений и представляемых ими языков.

Пример 5.2. Регулярное выражение (0 +1)^* представляет множество всех слов в алфавите {0, 1}.

Пример 5.3. Регулярное выражение 11(0 +1)^*001 представляет язык, состоящий из всех слов в алфавите {0, 1}, которые начинаются на '11', а заканчиваются на '001'.

Пример 5.4. Регулярное выражение представляет язык, состоящий из всех слов в алфавите {0, 1}, которые не содержат подслово '000' ( см. задачу 5.3).

Пример 5.5. Регулярное выражение 1^*(01^*01^*)^* представляет язык L_0ч, состоящий из всех слов в алфавите {0, 1}, в которых четное число нулей.

Действительно, каждое слово из L_0ч либо вообще не содержит нулей, т.е. входит в язык, представляющий 1^*, либо может быть разбито на блоки вида 01ⁱ01^j, i,j >= 0, которым, быть может, предшествует блок единиц. Выражение (01^*01^*), очевидно задает один такой блок, а его итерация - произвольную последовательность таких блоков.

Пример 5.6. Построим теперь регулярное выражение, представляющее язык L_0ч1ч, который состоит из всех слов в алфавите {0, 1}, содержащих четное число нулей и четное число единиц.

Пусть w=w₁w₂ ... w_n - произвольное слово из L_0ч1ч. Тогда, разумеется, n - четно, пусть n=2k. Разобьем w на пары соседних букв p_i =w_2i-1w_2i, i= 1,2,... ,k. Возможны 4 вида таких пар: 00, 11, 01 и 10. Пар вида 00 и 11 может быть сколько угодно, а пар вида 01 и 10 обязательно четное число. Поэтому w разбивается на блоки, каждый из которых начинается одной из пар 01 или 10 и содержит еще одну такую пару. Каждый такой блок описывается выражением (01 +10)(00 + 11)^*(01+10)(00 + 11)^*. При этом перед первым блоком может быть префикс, состоящий из пар 00 и 11. Множество слов состоящих из пар 00 и 11 задается выражением (00 +11)^*. Отсюда получаем выражение R_0ч1ч, задающее язык L_0ч1ч:

Дата добавления: 2015-07-26; просмотров: 165; Нарушение авторских прав

Мы поможем в написании ваших работ!