Задача на условный экстремум. Метод Эйлера—Лагранжа

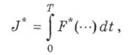
Помимо минимизируемого функционала

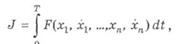
подынтегральная функция которого зависит от нескольких функций и их первых производных по времени, задано произвольное чнсло классических ограничений:

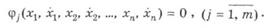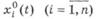
Требуется найти n экстремалей при заданных краевых условиях.

Метод решения этой задачи требует формирования нового функционала

где 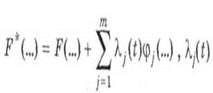- неизвестные функции, называемые множителями Лагранжа.

Благодаря такой замене задача сводится к предыдущей. При этом уравнения Эйлера должны быть составлены как для искомых экстремалей, так 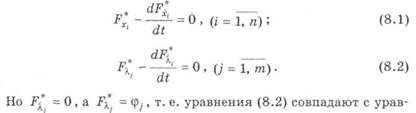нениями ограничений для множителей. Лагранжа

Поэтому может быть выполнено совместное решение системы уравнений Эйлера (8.1) и заданных ограничений. Исключая время из уравнений экстремалей, можно найти алгоритм управления оптималъного автоматического регулятора.-матричной фо:рме:

Дата добавления: 2015-07-26; просмотров: 214; Нарушение авторских прав

Мы поможем в написании ваших работ!