
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Метод динамического программирования
В основу метода динамического программирования положен принцип оптимальности. Согласно ему любой конечный отрезок оптимальной траектории (от произвольной промежуточной точки до одной и той же конечной точки процесса) является сам по себе оптимальной траекторией для своих краевых условий. Для доказательства предположим, что при движении по оптимальной траектории М0М1М20 (рис. 8.6) достигается минимум заданного критерия оптимальности.

Докажем, что конечный отрезок М1М20 является оптимальной траекторией для своих краевых условий. Допустим, что это не так, и минимум критерия оптимальности достигается при движении по траектории М1М’20. Но тогда и при движении из точки М0 меньшее значение критерия будет получено на траектории М0М1М’20, что противоречит первоначальному предположению и заставляет отвергнуть сделанное допущение.
Метод динамического программирования позволяет решать задачи трех видов: дискретную, дискретно-непрерывную и непрерывную.
Дискретная задача.Она отличается дискретностью всех величин (времени, управляющих воздействий, управляемых величин). К числу исходных данных относятся:
а) состояния выхода объекта управления;
б) значения управляющих воздействий;
в) алгоритм перехода из предыдущего состояния в последующее:
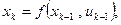
где 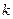 - номер шага,
- номер шага, 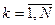 , причем эти переходы задаются таблицей или диаграммой переходов;
, причем эти переходы задаются таблицей или диаграммой переходов;
г) начальное состояние 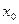 и число шагов процесса
и число шагов процесса 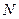 ;
;
д) критерий оптимальности 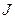 , зависящий от состояний и управлений в оптимальном процессе.
, зависящий от состояний и управлений в оптимальном процессе.
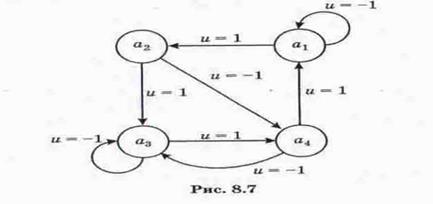
Пусть для выходная величина объекта может иметь четыре состояния:  . Управляющее воздействие может иметь два значения:
. Управляющее воздействие может иметь два значения: 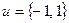 .
.
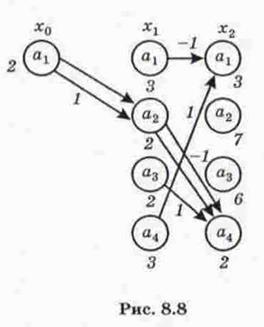
Диаграмма переходов показана на рис 8.7. Примем 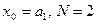 .
.
Критерий оптимальности управления объектом примем в виде функции от конечного состояния объекта 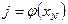 , которая задана таблично (табл. 8.1) и должна быть минимизирована.
, которая задана таблично (табл. 8.1) и должна быть минимизирована.
Таблица 8.1
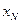
| 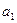
| 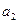
| 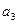
| 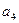
|
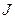
|
 Для решения задачи около каждого конечного состояния
Для решения задачи около каждого конечного состояния 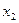 на диаграмме оптимальных переходов (рис. 8.8) записываем в соответствии с таблицей значения критерия оптимальности
на диаграмме оптимальных переходов (рис. 8.8) записываем в соответствии с таблицей значения критерия оптимальности 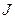 .
.
Затем рассматриваются все возможные переходы из каждого предыдущего состояния 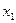 в последующие
в последующие 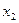 . Из них выбирается только те, которые оптимальны в смысле минимума
. Из них выбирается только те, которые оптимальны в смысле минимума 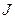 . Эти переходы отмечаются стрелками, около которых ставятся соответствующие значения управления, а около предшествующего состояния указывается значение
. Эти переходы отмечаются стрелками, около которых ставятся соответствующие значения управления, а около предшествующего состояния указывается значение 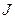 . После этого находится аналогично оптимальный переход из начального состояния
. После этого находится аналогично оптимальный переход из начального состояния 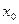 в
в 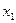 . Оптимальная траектория обозначена двойными стрелками и получается при управлении
. Оптимальная траектория обозначена двойными стрелками и получается при управлении

Дискретно-непрерывная задача МДП.В этой задаче управляющее воздействие и управляемые величины могут иметь бесчисленное количество значений в пределах заданных ограничений. Время изменяется дискретно с малым шагом 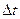 , что соответствует численным методам решения задач на ЭВМ. Задана продолжительность процесса Т, уравнение объекта управления
, что соответствует численным методам решения задач на ЭВМ. Задана продолжительность процесса Т, уравнение объекта управления
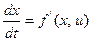 , (8.4)
, (8.4)
ограничение на управление 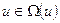 и начальное состояние
и начальное состояние 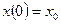 .
.
Задан в виде функционала минимизируемый критерий оптимальности
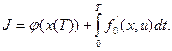 (8.5)
(8.5)
Требуется найти оптимальные управление 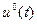 и траекторию
и траекторию 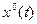 .
.
Прежде всего от дифференциального уравнения переходим к разностному уравнению, заменяя 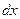 на
на 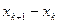 ,
, 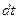 на
на 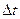 ,
, 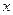 и
и 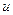 на
на 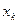 и
и 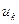 , где
, где 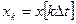 ,
, 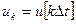 , относительное дискретное время k=0, 1, 2, …
, относительное дискретное время k=0, 1, 2, …
Обозначив 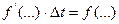 , получим из (8.4) разностное уравнение
, получим из (8.4) разностное уравнение
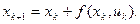 (8.6)
(8.6)
Критерий оптимальности (8.5) вместо интеграла необходимо представить в виде конечной суммы
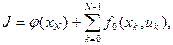 (8.7)
(8.7)
где 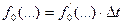 .
.
Переход к уравнениям (8.6) и (8.7) означает дискретизацию задачи по времени.
В соответствии с принципом оптимальности последовательно оптимизируем конечные отрезки процесса, начинающиеся от конечной точки 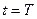 и постепенно увеличивающиеся на
и постепенно увеличивающиеся на 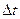 (рис. 8.9).
(рис. 8.9).
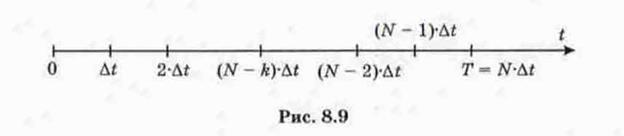
Первым рассматриваем отрезок
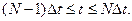
На этом отрезке из всего функционала (8.7) минимизируется частичная сумма
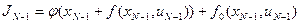
За счет изменения управления 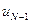 с учетом ограничений, где
с учетом ограничений, где 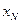 заменено согласно (8.6). В результате минимизации получаем следующую функцию от состояния
заменено согласно (8.6). В результате минимизации получаем следующую функцию от состояния 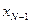 :
:
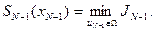 (8.8)
(8.8)
Данную зависимость необходимо запомнить до получения аналогичной функции на следующем шаге расчета. Кроме (8.8) определится и оптимальное управление
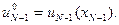 (8.9)
(8.9)
Функция (8.9) должна храниться в памяти до окончания расчета процесса. Затем переходим к отрезку  , на котором минимизируется
, на котором минимизируется
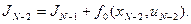
Минимум этой частичной суммы должен быть найден по двум переменным 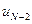 и
и 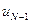 , но с учетом уже сделанной минимизации по
, но с учетом уже сделанной минимизации по 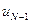 в виде (8.8) остается минимизировать ее только по одному аргументу
в виде (8.8) остается минимизировать ее только по одному аргументу 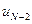 . В результате получим
. В результате получим
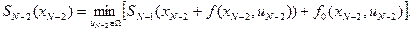
 (8.10)
(8.10)
Функция (8.10) заменяет в памяти функцию (8.8), и находится оптимальное управление

Аналогично на отрезке 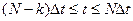 находим
находим
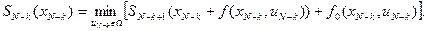
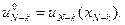
Наконец для всего процесса 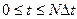 находим
находим
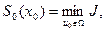
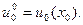 (8.11)
(8.11)
Таким образом, получен алгоритм расчета по рекуррентным формулам, который и называется динамическим программированием. При его применении по формуле (8.11) находим оптимальное управление 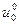 , затем по уравнению объекта (8.6) находим состояние объекта
, затем по уравнению объекта (8.6) находим состояние объекта 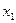 , далее находим
, далее находим 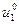 и т.д., вплоть до
и т.д., вплоть до 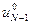 .
.
Метод динамического программирования.
В основе метода лежат сведение задачи оптимизации к задаче определения экстремальной траектории (минимальной или максимальной длины) в некоторой специальным образом построенном семействе возможных траекторий.
Принцип оптимальности Беллмана гласит: любой участок оптимальной траектории оптимален.
В случае дискретных задач метод динамического программирования
сводится к определению пути максимальной или минимальной длины в специальным образом построенной сети.
Дадим постановку задачи на примере классической задачи о ранце. Имеются n предметов. Каждый предмет имеет ценность 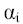 и вес сi. Требуется выбрать подмножество Q предметов так, чтобы их суммарная ценность
и вес сi. Требуется выбрать подмножество Q предметов так, чтобы их суммарная ценность
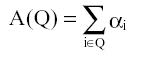
была максимальной при ограничении на суммарный вес
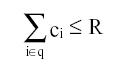
. Метод динамического программирования применим к ограниченному классу задач.
В настоящее время для решения оптимальных задач применяют в основном следующие методы:
-методы исследования функций классического анализа;
-методы, основанные на использовании неопределенных множителей Лагранжа;
-вариационное исчисление;
-динамическое программирование;
-принцип максимума;
-линейное программирование;
-нелинейное программирование.
Как правило, нельзя рекомендовать какой-либо один метод, который можно использовать для решения всех без исключения задач, возникающих на практике. Одни методы в этом отношении являются более общими, другие - менее общими. Наконец, целую группу методов (методы исследования функций классического анализа, метод множителей Лагранжа, методы нелинейного программирования) на определенных этапах решения оптимальной задачи можно применять в сочетании с другими методами, например динамическим программированием или принципом максимума.
Пожалуй, наилучшим путем при выборе метода оптимизации, наиболее пригодного для решения соответствующей задачи, следует признать исследование возможностей и опыта применения различных методов оптимизации.
| <== предыдущая страница | | | следующая страница ==> |
| Тестовые задания для самоконтроля. 1.Для решения задач оптимального управления применяются какие методыоптимизации | | | Тестовые задания для самоконтроля. 1. Основой метода динамического программирования является |
Дата добавления: 2015-07-26; просмотров: 212; Нарушение авторских прав

Мы поможем в написании ваших работ!