Синтез оптимальных систем с помощью вариационного исчисления

Фундаментальным понятием вариационного исчисления является функционал v, под которым понимают переменную величину, значение которой определяется выбором одной или нескольких функций. Например, функционалом v является длина кривой l, соединяющей две заданный точки А и В, расположенные на плоскости х0у,так как эта величина определяется выбором функции у(х), описывающей кривую, проходящую через эти точки, т.е.

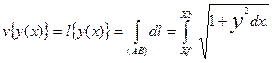
Другим примером функционала v может служит критерий эффективности системы Q, определяемый, частности, выражением (4.1), который зависит от вида функции у(х), описывающей переходные процессы в системе управления:

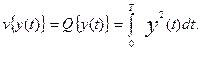
В общем случае зависимость, характерную для функционалов, можно сформулировать следующим образом: функции у(х) соответствует число v, определяющие значение функции.

Вариационное исчисление изучает методы исследования функционалов на максимум и минимум.

К вариационным задачам , прежде всего, относятся три классические задачи.

1.Задача о брахистохроне (см.пример 4.1)

2.Геодезическая задача, в которой требуется определить линию наименьшей длины l, соединяющую две заданные точки на некоторой поверхности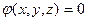

3.Изопериметрическая задача, в которой требуется найти уравнение замкнутой линии заданной длины L, ограничивающей максимальную площадь S.

Эта вариационная задача была решена еще в Древней Греции: такой замкнутой линией оказалась окружность.

Заметим, что в последних двух задачах экстремум функционала ищется при определенных условиях 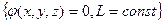. Поэтому такие задачи называются задачами на условный экстремум.

Методы решения вариационных задач весьма сходны с методами исследования функции на максимум и минимум. В частности, если функционал, например, 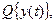достигает экстремума при у(t)=y_э(t), то вариация функционала 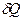,под которой понимают линейную часть его приращения по отношению к приращению функции y(t), равна нулю, то есть

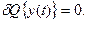
Здесь y_э(t) -это функция, принадлежащая к некоторому классу функций, при которой значение функционала Q достигает экстремума.

Именно поэтому функция y_э(t) называется экстремалью функционала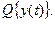

В теории вариационного исчисления доказывается, что если функционал задан в виде

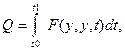то экстремаль функционала y(t,C₁,C₂), где С₁,С₂- постоянные интегрирование, определяемые из граничных условий y(t₀),y(t₁), является решением уравнения Эйлера:

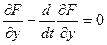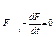или (4.5)

Проиллюстрируем методику решения вариационных задач на одном классическом примере.

Дата добавления: 2015-07-26; просмотров: 218; Нарушение авторских прав

Мы поможем в написании ваших работ!