Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
Регулярные методы поиска экстремума
В регуляторных методах выбор направления поискового движения осуществляется по заранее заданному закону.
§ Сканирование (полный перебор) используют только в том случае, если имеется информация только о наличии свойства экстремальности у функционала J(x) и о необходимости выполнения условия (см. рис.3.2) J(x*)£ J(x). Здесь А–допустимый интервал х (изменения управляемого параметра). Необходимо также задаться точностью достижения экстремума e>0, которой в основном и определяется длительность процедуры поиска.
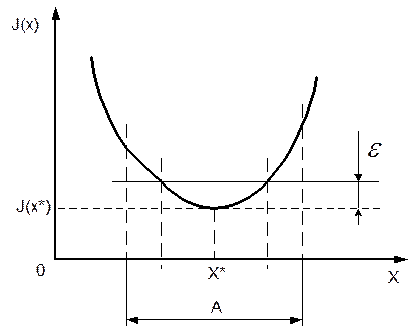
Рис.3.2. К методу сканирования
§ Метод Гаусса–Зайделя использует дополнительную априорную информацию о виде функционала качества J(х). Например, предполагают, что J(х) является унимодальной функцией. Для поиска минимума условие унимодальности:
Здесь хmin–положение точки минимума; х1, х2 – произвольные положения относительно точки минимума (см. рис. 3.3).
Рис.3.3. К методу Гаусса-Зайделя
В основу рассматриваемого метода положено исследование полной производной функционала
где 
Здесь аli – коэффициенты, которые характеризуют отклонение функционала от экстремума.
Таким образом
(3.1)
В точке экстремума (xi=xextr) получим 
и поэтому во всех точках, кроме xextr, функция (3.1) должна удовлетворять условию монотонного приближения к экстремуму, т.е.
Процедура Гаусса–Зайделя такова.
1) Производят поочередное изменение координат xi и определяют частные экстремумы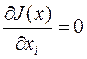 
по каждой координате (при этом все координаты кроме выбранной закрепляют).
2) После обращения в нуль, например,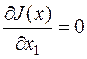 
, полученное значение х1 закрепляют и изменяют х2 и т.д. Таким образом находят частные экстремумы по всем координатам.
3) Осуществляют повторный цикл до тех пор, пока найденная точка экстремума не окажется экстремальной для всех координат.
Пример 3.1. Пусть задана функция качества
Найти экстремум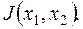 
Решение
1) Начинаем поиск из точки 1 (см. рис.3.4) х1=3; х2=3, причем изменяем координату х1, а х2 закрепляем.
Функция качества
(3.2)
Находим минимум, приравняв нулю частную производную:
Отсюда первый экстремум по х1 точка 2
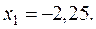
Координаты точки 2 (–2,24; 3).
2) Закрепляем х1= –2,25 и изменяем х2.
Находим минимум по х2:
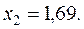
Получаем координаты точки 3: (–2,25; 1,69).
3) Повторяем цикл для координаты х1, закрепляем х2=1,69.
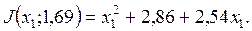
В результате получим ломаную линию из взаимно перпендикулярных прямых, как это видно на рис.3.4. Точки излома находятся в местах касания с кривыми 
.(на этом же рисунке иллюстрируется для сравнения и метод наискорейшего спуска, о котором речь пойдет далее).
Существенным недостатком метода Гаусса-Зайделя является произвольность в выборе нумерации координат, что может привести к удлинению поиска.
§ Метод градиента. Градиентом выпуклой дифференцируемой функции 
называется вектор, проекции которого на оси координат 
соответственно равны частным производным 
и т.д. Пусть задана функция 
. Каждая из составляющих градиента может быть оценена (приближенно определена) по двум измерениям значений в близких точках 
:
.
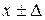Если функция зависит от нескольких переменных, то градиент определяют по всем переменным.
После определения направления градиента переходят в новое положение по каждой координате в зависимости от максимальной величины и направления градиента. В этом методе используют свойство уменьшения величины градиента по мере приближения к экстремуму. Это можно проследить на рис.3.5, наблюдая за изменением наклона касательных к кривой .
Процесс поиска разделяют на два этапа. Сначала делают пробный шаг для определения величины и направления градиента по алгоритму
где x0 – координата вектора начального состояния;
х – то же пробного состояния;
g– величина пробного шага;
– единичный вектор отклонения по заданной координате.
Затем делают одновременное смещение в направлении градиента всех координат в соответствии с уравнением
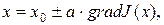
где а – величина рабочего шага;
х – вектор нового рабочего состояния.
Рис.3.4. Поиск экстремума функционала качества
§ Метод наискорейшего спуска. В методе градиента кривые движения нормальны к линиям постоянного значения функции качества . При наличии так называемых “оврагов” и “гребней” движение по градиенту может стать извилистым и поиск может значительно затянуться (см. рис.3.7, движение из точки А). В методе наискорейшего спуска также определяют градиент в исходной точке, а затем движение происходит по выбранному направлению до тех пор, пока функция качества продолжает уменьшаться. Затем вновь определяют направление и продолжают движение по новой прямой (см. движение из точки В на рис.3.6).
Рис.3.5. Градиентный метод
Пример 3.2. Задана та же функция качества, что и в примере 3.1:
(3.3)
Требуется найти минимум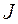 
методом наискорейшего спуска.
Решение
Пусть в исходной точке 
· 1-ая итерация
a) Находим частные производные в точке (2;3)
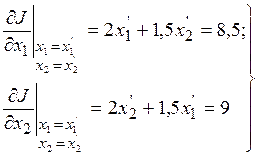(3.4)
Рис.3.6. Пояснение метода наискорейшего спуска
b) Координаты следующей точки найдем, двигаясь в направлении, обратном полученному градиенту:
(3.5)
Здесь а – шаг перехода из точки 
в точку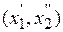 
, величина которого пока неизвестна.
c) Определяем а, подставляя (3.5) в (3.3).
С учетом (3.5)
Находим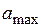 
из условия
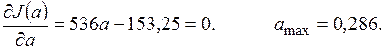
d) Подставляя 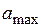в (3.5), находим координаты точки 
:
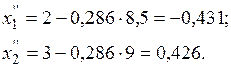
· 2-ая итерация
a) Находим частные производные в точке (-0,431; 0,426)
b) 
c) .
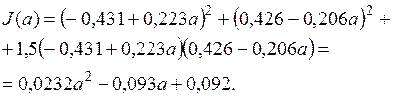
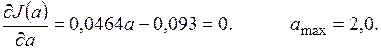
d)
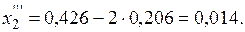
Система практически обеспечила достижение минимума функции качества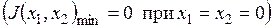 
.
На рис.3.5 показана траектория движения. Очевидно, что метод наискорейшего спуска эффективнее метода Гаусса–Зайделя, т.к. практически за две итерации поиска система оказалась достаточно близко к минимуму.
| <== предыдущая страница | | | следующая страница ==> |
| Общая характеристика СНС | | | Методы случайного поиска экстремума |
Дата добавления: 2015-07-26; просмотров: 501; Нарушение авторских прав
Мы поможем в написании ваших работ!