Уравнения, содержащие переменную под знаком модуля

1º. Модуль (абсолютная величина) числа а определяется следующим образом:

.

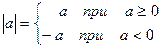Геометрический смысл модуля: |a| есть расстояние от точки числовой оси, изображающей данное число а, до начала отсчета - точки О, а |x-a| есть расстояние между точками числовой оси, соответствующими числам х и а.

2º. Уравнения вида 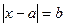можно решать геометрически.

Рассмотрим аналитические способы решения уравнений, содержащих переменную под знаком модуля, на примерах.

При решении уравнений важно уметь в соответствии с определением модуля освободиться от вертикальных скобок.

Например, 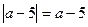, если a ≥ 5;

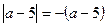, если a < 5.

Пример 4. Решим уравнение 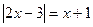, используя определение модуля числа.

Решение: Уравнение имеет решение, если x+1≥0, т.е. x≥-1.

.

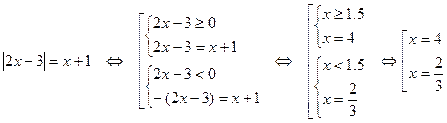Условие x≥-1 выполняется в обоих случаях.

Ответ: 4; 2/3.

Пример 5. Решим уравнение 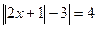, используя свойство модулей («модули противоположных чисел равны»).

Решение:

.

1) |2x+1|=7 => 2x+1=7 или 2x+1=-7 => x=3 или x=-4

2) |2x+1|-3=-4 => |2x+1|=-1 – нет решений.

Ответ: 3; -4.

Пример 6. Решим уравнение 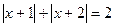, рассматривая решения на интервалах.

Решение: Найдем нули модулей, т.е. такие значения x, при которых 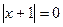и : .

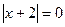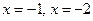Рассмотрим уравнение на интервалах (-∞; -2), [-2; -1), [-1; +∞).

а) Для 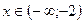уравнение примет вид:

-(x+1)-(x+2)=2; -x-1-x-2=2; -2x=5; x=-2,5; 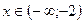=> x=-2,5 – корень уравнения.

б) Для 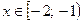уравнение примет вид:

-(x+1)+(x+2)=2; -x-1+x+2=2; 0·x=1- нет корней.

в) Для 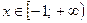уравнение примет вид:

x+1+x+2=2; 2x=-1; x=-0,5; 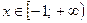=> x=-0,5 – корень уравнения.

Ответ: -2,5; -0,5.

Дата добавления: 2015-07-26; просмотров: 324; Нарушение авторских прав

Мы поможем в написании ваших работ!