Функции нескольких переменных. Теорема 3.4. Для того, чтобы функция была дифференцируемой в точке М (x, y), она должна быть непрерывной и иметь непрерывные частные производные в этой

Теорема 3.4. Для того, чтобы функция была дифференцируемой в точке М (x, y), она должна быть непрерывной и иметь непрерывные частные производные в этой точке.

Д о к а з а т е л ь с т в о. Запишем полное приращение функции

.

В правой части прибавим и вычтем , получим

.

По теореме Лагранжа о конечном приращении

, где ,

, где .

Тогда

.

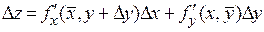Так как частные производные по условию теоремы непрерывны, то

, .

Используя теорему 1.3 о представлении функции в виде суммы предела и бесконечно малой функции, запишем

, ,

где 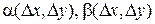- бесконечно малые функции при .

Учитывая эти выражения, получим

или

.

В соответствии с определением дифференцируемости функции это означает, что функция является дифференцируемой.

Следствие. Для того, чтобы установить дифференцируемость функции, нужно проверить непрерывность частных производных.

Дата добавления: 2015-07-26; просмотров: 252; Нарушение авторских прав

Мы поможем в написании ваших работ!