Дифференциал функции

1. Понятие дифференциала.

2. Применение дифференциала к приближенным вычислениям.

3. Дифференциалы высших порядков.

-1-

Пусть функция y=f(x) имеет в точке х отличную от нуля производную 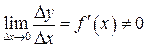. Тогда по теореме о связи функции, ее предела и бесконечно малой функции, можно записать , где при , или .

Таким образом, приращение функции представляет собой сумму двух слагаемых и , являющихся бесконечно малыми при . При этом первое слагаемое есть бесконечно малая функция одного порядка с , т.к. , а второе слагаемое есть бесконечно малая функция более высокого порядка, чем :

.

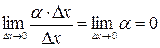Поэтому первое слагаемое называют главной частью приращения функции ∆у.

Определение. Дифференциалом функции y=f(x) в точке х называется главная линейная относительно ∆х часть приращения функции, равная произведению производной функции на приращение аргумента, и обозначается dy (или df(x)):

. (1)

Пример 1. Найти дифференциал функции .

Решение: По формуле находим

.

Геометрический смысл дифференциала функции.

Проведем к графику функции y=f(x) в точке М(х;у) касательную МТ и рассмотрим ординату этой касательной для точки . На рис. . Из треугольника МАВ имеем , то есть .

Но, согласно геометрическому смыслу производной, . Поэтому Сравнивая полученный результат с формулой (1), получаем dy=AB, т.е. дифференциал функции y=f(x) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение .

- 2 -

Как уже известно, приращение Δу функции y=f(x) в точке х можно представить в виде , где при , или 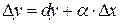. Отбрасывая бесконечно малую более высокого порядка, чем Δx, получаем приближенное равенство

(2)

причем это равенство тем точнее, чем меньше Δx.

Это равенство позволяет с большей точностью вычислить приближенно приращение любой дифференцируемой функции.

Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (2) широко применяется в вычислительной практике.

Подставляя в равенство значения Δу и dy, получим

или

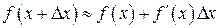(3)

Формула (3) используется для вычислений приближенных значений функций.

Пример 4. Вычислить приближенно arctg 1,05.

Решение: Рассмотрим функцию f(x)=arctg x. По формуле (3) имеем:

т.е. .

Так как x+Δx=1.05, то при х=1 и Δх =0.05 получаем:

-3-

Пусть y=f(x) дифференцируемая функция, а ее аргумент х – независимая переменная. Тогда ее первый дифференциал - есть также функция и можно найти дифференциал этой функции.

Дифференциал от дифференциала функции y=f(x) называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается .

Итак, по определению d²y=d(dy). Найдем выражение второго дифференциала функции y=f(x).

Так как dx=Δx не зависит от х, то при дифференцировании считаем dx постоянным и можно выносить за знак дифференциала.

т.е. . (4)

Аналогично определяется и находится дифференциал третьего порядка:

И, вообще, дифференциал n-го порядка есть дифференциал от дифференциала (n-1)-го порядка:

Отсюда находим, что . В частности, при n = 1,2,3 соответственно получаем

т.е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

Пример 5. Найти d²y, если y=e^3x и х – независимая переменная.

Решение: Так как то по формуле (4) имеем .

Дата добавления: 2015-07-26; просмотров: 328; Нарушение авторских прав

Мы поможем в написании ваших работ!