
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Правила дифференцирования
1. Правила дифференцирования.
2. Производные сложной и обратной функций.
3. Производные основных элементарных функций, таблица производных.
4. Производные высших порядков.
- 1 -
Нахождение производной функции непосредственно по определению часто связано с определенными трудностями. На практике функции дифференцируют с помощью ряда правил и формул.
Пусть функции u=u(x) и  - две дифференцируемые на некотором интервале (a;b) функции.
- две дифференцируемые на некотором интервале (a;b) функции.
Теорема 1. Производная суммы (разности) двух функций:
 . (1)
. (1)
Теорема справедлива для любого конечного числа слагаемых.
Теорема 2. Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго:
 . (2)
. (2)
Следствие 1. Постоянный множитель можно выносить за знак производной: 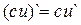 .
.
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, например:  .
.
Теорема 3. Производная частного двух функций  , если
, если  ≠0 равна дроби, числитель который есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя.
≠0 равна дроби, числитель который есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя.
 . (3)
. (3)
Следствие 3.  .
.
Следствие 4.  , где с = const.
, где с = const.
Пример 1. Найти производную функции  и вычислить ее значение в точке х=1.
и вычислить ее значение в точке х=1.
Решение. 
Значение производной в точке х=1 есть  .
.
- 2 -
Пусть переменная y есть функция от переменной u , то есть у=f(u), а переменная u в свою очередь есть функция от независимой переменной х, то есть 
 задана сложная функция
задана сложная функция  .
.
Теорема 4. Если функция  имеет производную
имеет производную  в точке х, а функция у=f(u) имеет производную
в точке х, а функция у=f(u) имеет производную  в соответствующей точке
в соответствующей точке  , то сложная функция
, то сложная функция  имеет производную
имеет производную  в точке х, которая находится по формуле
в точке х, которая находится по формуле
 . (4)
. (4)
Итак, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.
Это правило остается в силе, если промежуточных аргументов несколько. Так, если у=f(u),  ,
,  , то
, то  .
.
Пусть y=f(x) и 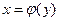 - взаимно-обратные функции.
- взаимно-обратные функции.
Теорема 5. Если функция y=f(x) строго монотонна на интервале (a;b) и имеет неравную нулю производную 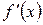 в произвольной точке этого интервала, то обратная ей функция
в произвольной точке этого интервала, то обратная ей функция 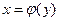 также имеет производную
также имеет производную  в соответствующей точке, определяемую равенством
в соответствующей точке, определяемую равенством
 или
или  .
.
Таким образом, производная обратной функции равна обратной величине производной данной функции.
Пример 2. Найти производную функции  .
.
Решение. Данная функция является сложной. Ее можно представить в виде цепочки простых функций:  , где
, где  , где
, где  , где
, где  . По правилу дифференцирования сложной функции
. По правилу дифференцирования сложной функции  получаем
получаем 
Пример 3. Пользуясь правилом дифференцирования обратной функции, найти производную  для функции
для функции 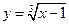 .
.
Решение. Обратная функция  имеет производную
имеет производную  . Следовательно
. Следовательно
 .
.
- 3 -
Таблица производных элементарных функций
| № п/п | Функция у | Производная | № п/п | Функция 
| Производная | |
| с | 
| 
| ||||
| х | 
| 
| ||||

| 
| 
| 
| |||

| 
| 
| 
| |||
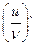
| 
| 
| 
| |||

| 
| 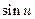
| 
| |||

| 
| 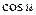
| 
| |||

| 
| 
| 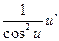 
| |||

| 
| 
| 
| |||
 , , 
| 
| 
| 
| |||

| 
| 
| 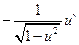
| |||

| 
| 
| 
| |||

| 
| |||||
-4-
Производная  функции y=f(x) есть также функция от х и называется производной первого порядка.
функции y=f(x) есть также функция от х и называется производной первого порядка.
Если функция  дифференцируема, то ее производная называется производной второго порядка и обозначается
дифференцируема, то ее производная называется производной второго порядка и обозначается  (или
(или  . Итак,
. Итак,  .
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается  .
.
Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:
 .
.
Производные порядка выше первого называются производными высших порядков.
Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (yV или y(5)).  .
.
| <== предыдущая страница | | | следующая страница ==> |
| Задача о производительности труда | | | Дифференциал функции |
Дата добавления: 2015-07-26; просмотров: 228; Нарушение авторских прав

Мы поможем в написании ваших работ!