Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения

Дифференциальное уравнение вида

(1)

называется уравнением с разделёнными переменными. Его общим интегралом будет

, где С – произвольная постоянная

Уравнение вида

(2)

или

, (3)

а также уравнения, которые с помощью алгебраических преобразований приводятся к уравнениям (2) или (3), называются уравнениями с разделяющимися переменными.

Уравнение вида (2) путём деления на произведение приводится к уравнению с разделёнными переменными:

.

Его общий интеграл имеет вид:

.

Замечание: Деление на может привести к потере частных решений, обращающих в ноль произведение . То есть, необходимо проверить, являются ли корни уравнений и решениями исходного дифференциального уравнения.

Дифференциальное уравнение вида

,

где a, b и с – постоянные, заменой переменных приводится к уравнению с разделяющимися переменными.

Пример 1.Найти общее решение дифференциального уравнения

Пусть .

Разделив обе части уравнения на , получим уравнение с разделенными переменными:

или

.

Последнее равенство является общим интегралом исходного уравнения.

При его нахождении были приняты ограничения . Однако, функции и также являются решениями исходного уравнения, что легко проверяется; с другой стороны, их можно получить из общего интеграла при . Следовательно, и - частные решения исходного уравнения.

Ответ:

Пример 2. Найти частное решение уравнения , удовлетворяющее начальному условию .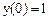

Запишем данное уравнение в дифференциальной форме:

Заметим, что 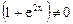. Разделяя переменные, получим:

Проинтегрируем последнее уравнение:

или .

Получили общее решение исходного уравнения.

Использовав начальное условие, определим значение произвольной постоянной С:

Следовательно, частное решение исходного уравнения имеет вид

Ответ: .

Дифференциальное уравнение вида: или называется однородным относительно переменных x и y, если f(x, y) – однородная функция нулевого измерения относительно своих аргументов, то есть выполняется равенство: .

Однородное уравнение при помощи замены: , где - новая функция, сводиться к уравнению с разделяющимися переменными относительно и функции ( ).

Дата добавления: 2015-07-26; просмотров: 224; Нарушение авторских прав

Мы поможем в написании ваших работ!