Пример 3. Это уравнение не будет уравнением с разделяющимися переменными

Решить уравнение: .

Это уравнение не будет уравнением с разделяющимися переменными. Заметим, что правая часть этого уравнения - есть однородная функция нулевого измерения относительно переменных x и y. Действительно, выполняется равенство: . Значит наше уравнение является однородным. Введём замену , тогда .Подставляя в исходное уравнение выражения для и , получим:

.

Разделяя переменные, приходим к уравнению: . Интегрируя его, получим:

Ответ: .

Пример 4.Решить уравнение

Решение. Запишем уравнение в виде

.

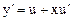Данное уравнение однородное относительно x и y. Пусть . Тогда . Подставляя в исходное уравнение выражения для и , получим

.

Разделяя переменные:

.

Интегрируя, находим

или .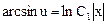

Так как 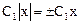, то, обозначая , получаем 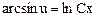, где или . Заменяя u на ,получим общий интеграл

.

Отсюда общее решение: .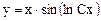

При разделении переменных мы делили обе части уравнения на произведение , поэтому могли потерять решения, которые обращают в ноль произведение.

Положим теперь 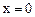и . Но в силу подстановки , а из соотношения получаем, что , откуда . Непосредственной подстановкой убеждаемся, что функция и также являются решениями данного уравнения.

Ответ: , .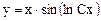

Примечание. Уравнения вида

где a, b - некоторые числа, приводятся к уравнению с разделяющимися переменными с помощью замены:

(или , где с - число).

Дата добавления: 2015-07-26; просмотров: 197; Нарушение авторских прав

Мы поможем в написании ваших работ!