Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Частным случаем рассмотренных выше линейных однородных дифференциальных уравнений являются линейные однородные дифференциальные уравнения с постоянными коэффициентами.

Пусть дано ЛОДУ второго порядка

,

(1)

где и постоянны.

Для нахождения общего решения уравнения (1) достаточно найти два его частных решения, образующих фундаментальную систему.

Будем искать частные решения уравнения в виде

,

где − некоторое число (предложено Л.Эйлером). Дифференцируя функцию два раза и подставляя выражения для , 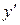и в уравнение (1), получим:

, т.е.

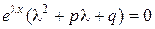, или

.

(2)

Уравнение (2) называется характеристическим уравнением дифференциального уравнения (1) (для его составления достаточно в уравнение (1) заменить , 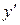и соответственно на , и 1).

В зависимости от природы корней характеристического уравнения придется рассмотреть три случая:

Случай 1. Корни характеристического уравнения (2) действительные и различные: .

В этом случае частными решениями уравнения (1) являются функци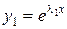и и . Они образуют фундаментальную систему решений (линейно независимы), так как вронскиан

.

Следовательно, общее решение уравнения (1), согласно теореме 3, имеет вид:

.

(3)

Пример 1. Решить уравнение: .

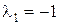Решение: Составим характеристическое уравнение: . Решаем его: , . Записываем общее решение данного уравнения 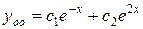, где и произвольные постоянные.

Ответ: .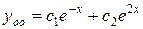

Случай 2. Корни и характеристического уравнения (2) действительные и равные: , .

В этом случае имеем лишь одно частное решение .

Покажем, что наряду с решением уравнения (1) будет функция .

Действительно, подставим функцию в уравнение (1). Имеем: , .

.

Здесь, , так как есть корень уравнения (2); , так как по условию .

То есть функция является решением уравнения (1).

Частные решения и образуют фундаментальную систему решений: , действительно:

.

Следовательно, в этом случае общее решение ЛОДУ (1) имеет вид:

.

(4)

Пример 2. Решить уравнение: .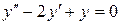

Решение: Составим характеристическое уравнение: . Решаем его: . Записываем общее решение данного уравнения , где и произвольные постоянные.

Ответ: .

Случай 3. Корни и уравнения (2) комплексные: , .

По формуле Эйлера: .

Рассмотрим функцию , так как второй случай отличается несущественно .

Убедимся, что − решение дифференциального уравнения (1).

,

.

Подставляя производные и функцию , в левую часть линейного однородного уравнения получаем:

.

Здесь применена теорема Виета, в нашем случае: , .

Аналогично для функции .

Осталось проверить, что функции и образуют фундаментальную систему решений: , , , .

,

так как , ( − комплексное число, а его мнимая часть).

Следовательно, в этом случае общее решение ЛОДУ (1) имеет вид:

, или

.

(5)

Пример 3. Решить уравнение: .

Решение: Составим характеристическое уравнение: . Решаем его: , . По формуле (5) получаем общее решение уравнения:

Ответ: .

Таким образом, нахождение общего решения ЛОДУ второго порядка с постоянными коэффициентами (1) сводится к нахождению корней характеристического уравнения (2) и использованию формул (3)−(5) общего решения уравнения (не прибегая к вычислению интегралов).

Дата добавления: 2015-07-26; просмотров: 288; Нарушение авторских прав

Мы поможем в написании ваших работ!