Линейные однородные дифференциальные уравнения третьего порядка с постоянными коэффициентами

Уравнение вида

,

(1)

где , , постоянные числа называется линейным однородным дифференциальным уравнением третьего порядка с постоянными коэффициентами.

Данное уравнение решается аналогично случаю уравнению второго порядка с постоянными коэффициентами.

Характеристическим для уравнения (1) является алгебраическое уравнение третьего порядка вида

.

(2)

Уравнение (2) имеет, как известно три корня (в том числе могут быть и комплексные!). Обозначим их , и .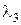

Рассмотрим четыре возможных случая для корней характеристического уравнения (2).

Случай 1. Все три корня характеристического уравнения (2) действительные и различные: , , , .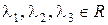

В этом случае общее решение ЛОДУ (1) имеет вид:

.

(3)

Пример 1. Найти общее решение уравнения .

Решение: Характеристическое уравнение имеет корни 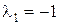, , 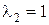. Так как все корни характеристического уравнения действительные и различные, то применим формулу (3). Следовательно, общее решение уравнения имеет вид: .

Ответ: .

Случай 2. Все три корня характеристического уравнения (2) действительные и два из них совпадают: , , .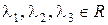

В этом случае общее решение ЛОДУ (1) имеет вид:

.

(4)

Пример 2. Найти общее решение уравнения .

Решение: Составим характеристическое уравнение , один из корней которого можно получить методом проб.

Так как , то уравнение принимает вид , откуда , Таким образом, характеристическое уравнение имеет три действительных корня, два из которых совпадают. Тогда согласно формуле (4) общее решение дифференциального уравнения имеет вид: .

Ответ: .

Случай 3. Все три корня характеристического уравнения (2) действительные и совпадающие: , .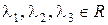

В этом случае общее решение ЛОДУ (1) имеет вид:

.

(5)

Пример 3. Найти общее решение уравнения .

Решение: Составим характеристическое уравнение , решая его получаем, . Таким образом, характеристическое уравнение имеет три действительных и совпадающих корня, тогда согласно формуле (5) общее решение дифференциального уравнения имеет вид: .

Ответ: .

Случай 4. Один из корней характеристического уравнения (2) действительный и два комплексных: , , , .

В этом случае общее решение ЛОДУ (1) имеет вид:

.

(6)

Пример 4. Найти общее решение уравнения .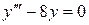

Решение: Составим характеристическое уравнение , решая его получаем, , , . Таким образом, характеристическое уравнение имеет один действительный и два комплексных корня, тогда согласно формуле (6) общее решение дифференциального уравнения имеет вид: .

Ответ: .

Дата добавления: 2015-07-26; просмотров: 208; Нарушение авторских прав

Мы поможем в написании ваших работ!