Решение неоднородных линейных уравнений второго порядка методом вариаций произвольных констант

Пусть дано линейное неоднородное дифференциальное уравнение (ЛНДУ):

.

(1)

Предположим, что общее решение соответствующего однородного уравнения уже известно и имеет следующий вид: . Тогда на основании теоремы 4 (пункт 1.10) решение ЛНДУ имеет вид: . Таким образом осталось найти какое-либо решение неоднородного уравнения . Лагранж (Жозеф Луи 1736-1813, французский математик и механик) предложил искать функцию в том же виде, что и с той лишь разницей, что и уже не является константами, а некоторые функции переменной , подбор которых и должен обеспечить обращение неоднородного уравнения в верное равенство, при подстановке в него функции . Так как функции и подбираются произвольно, то этот метод называется метод вариаций произвольных констант.

(переменную опустим),

.

Так как функций и выбираются произвольно, то пусть они выбраны так, что . Значит

.

Подставим , и в уравнение (1):

.

Первые производные неизвестных функций являются решением системы: .

Главный определитель этой системы является вронскианом и он отличен от нуля на основании теоремы 2 пункт 1.10, значит система имеет единственное решение и . Для нахождения функций и нужно решить пару дифференциальных уравнений первого порядка.

Замечание. Метод Лагранжа имеет неудобство, связанное с вычислением двух интегралов для нахождения функций и , так как интегралы могут оказаться сложными.

Пример. Найти общее решение уравнения .

Решение: Решение уравнения будем искать в виде: . Найдем сначала . Характеристическое уравнение имеет корни: 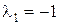, , 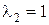значит .

Для нахождения воспользуемся методом вариации произвольных констант.

Будем искать частное решение исходного уравнения в виде , где и − неизвестные пока функции, подлежащие определению. Для их нахождения имеем систему

,

то есть

.

Решая систему относительно и , получим:

, .

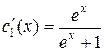Отсюда интегрируя, находим:

, .

Подставляя функции и в решение, получим

или

.

Общим решением исходного уравнения будет

,

где и − произвольные постоянные.

Ответ: .

Дата добавления: 2015-07-26; просмотров: 207; Нарушение авторских прав

Мы поможем в написании ваших работ!