Упруго-пластический изгиб бруса

Рассмотрим упруго-пластический чистый изгиб бруса. Для простоты предполагается, что поперечное сечение бруса обладает двумя осями симметрии (рис.22.3, а) и что диаграмма деформирования материала при одноосном сжатии и растяжении одинаковы (рис.22.3, б). При принятых предположениях следует полагать, что нейтральная линия совпадает с осью симметрии x (рис.22.3, а) (Диаграмма Прандтля).

Как и при упругом изгибе в данном случае будет исходить, что и при упруго-пластическом изгибе справедлива гипотеза плоских сечений, т.е.:

, (22.26)

где 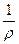- кривизна нейтральной оси изогнутого бруса, а y - расстояние точек от нейтральной оси.

Рис.22.3

Упруго-пластическая стадия деформирования поперечного сечения бруса делится на две зона: упругую и пластическую. Величина 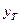, определяющая расстояние границы этих зон от нейтральной линии определяется по (22.26):

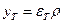. (22.27)

По мере увеличения изгибающего момента и соответственно кривизны, величина 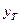уменьшается за счет сокращения высоты упругой зоны.

Выражение изгибающего момента в данном случае можно преобразовать в следующем виде:

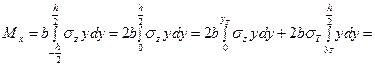
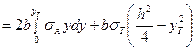. (22.28)

Так как из теории изгиба, для упругого участка, выполняется соотношение:

.

Подставляя последнее в (22.28) и после интегрирования получим:

.

Учитывая, что 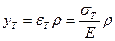, получим:

,

откуда

.

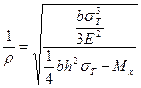Из последнего выражения следует, что кривизна бруса с увеличением момента М_x возрастает и обращается в бесконечность, при

. (22.29)

В этом случае 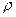= 0, следовательно, и как это следует из (22.27) 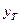= 0. Следовательно, все сечение охватывается пластической деформацией. Несущая способность сечения в данном случае исчер­пана. Из (22.29) можно определить:

.

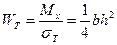Здесь носит название пластического момента сопротивления сечения.

Обобщая выражения (22.29) с известным аналогичным соотношением теории изгиба 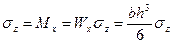, можно установить, что при значениях момента в поперечном сечении балки возникает пластическая деформация, а значение следует рассматривать как предельное значение момента, при котором несущая способность конструкций в данном сечении исчерпана.

Дата добавления: 2015-07-26; просмотров: 359; Нарушение авторских прав

Мы поможем в написании ваших работ!