Упруго-пластический расчет стержня при действии продольной силы

Рис.22.2

Определить перемещение сечения А ступенчатого стержня изображенного на рис.22.2, а при различных стадиях его деформирования при нагружении его силой Р. Диаграмма деформирования изображена на рис.22.2, б.

Решение:

В данном случае все составляющие тензора напряжений и деформаций за исключением s_х и e_х тождественно равны нулю. При этом участок АС испытывает растяжения, а участок АВ - сжатие.

Следует выделить следующие этапы работы конструкций.

На первом этапе, участки АС и АВ деформируются в упругой стадии, т.е.:

при . (22.8)

На втором этапе, один из участков АВ или АС переходит в упруго-пластическую стадию деформирования. И, наконец, когда оба участка АВ и АС деформируются в упруго-пластической стадии.

Связь между s_х и e_х в упруго-пластической стадии деформирования согласно диаграмме s~e записывается в виде:

при . (22.9)

На первом этапе нагружения, когда в обоих участках материал конструкции деформируется по закону Гука, учитывая, что система один раз статически неопределима усилия N обоих участков определяется обычными приемами. Из условий равновесия имеем:

-N₁ + N₂ = P. (22.10)

Учитывая, что стержни верхним и нижним концами жестко закреплены, его абсолютное удлинение должно быть равно нулю, т.е.:

,

откуда

. (22.11)

В результате совместного рассмотрения (22.10) и (22.11) получим:

(22.12)

Перемещение сечения А будет следующим:

. (22.13)

В упругой стадии работы конструкции значения напряжения на первом и втором участках соответственно принимают значения:

. (22.14)

Так как 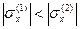, то соотношения (22.12¸22.14) будут справедливы до тех пор, пока напряжения на первом участке не достигнет значения .

Из выражения (22.14), принимая , определяем величину силы Р, при которой нижний участок с номером I переходит в пластичное состояние, а верхний участок с номером II остается упругим:

. (22.15)

Для второго этапа нагружения, необходимо преобразовать уравнения совместности деформаций:

. (22.16)

Выражение (22.9) представим в виде:

. (22.17)

Тогда

. (22.18)

Подставляя (22.18) в (22.16) получим:

. (22.19)

Совместно решая (22.19) с уравнением равновесия (22.10) получим:

(22.20)

Принимая в (22.20) Е = Е₁, можно убедиться, что из (22.20) следуют упругие решения (22.14).

Перемещая сечения А на данном этапе нагружения определяется по формуле:

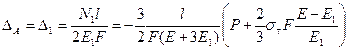. (22.21)

Переходим к решению поставленной задачи на третьем этапе нагружения. Принимая из второго выражения (22.14) определим значения внешней силы при которой второй участок переходит в пластическую стадию деформирования:

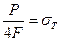, откуда 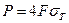. (22.22)

На третьем этапе нагружения, т.е. 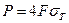абсолютное удлинение второго участка определяется:

. (22.23)

Подставляя (22.23) и (22.18) в (22.16) получим:

. (22.24)

В результате совместного рассмотрения (22.24) и (22.10) определяется:

. (22.25)

Принимая Е = Е₁ из (22.25) получим решение задачи в упругой постановке, которая полностью согласуется выражением (22.12). Перемещение сечения А на третьем этапе нагружения определяется по выражению:

Если в последнем варианте предположить Е = Е₁, то отсюда следует решение в упругой постановке задачи, и полностью совпадающей с решением (22.13).

Дата добавления: 2015-07-26; просмотров: 282; Нарушение авторских прав

Мы поможем в написании ваших работ!