Практическая работа № 1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН

КАРАГАНДИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

А.В. Олейникова

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ПРАКТИЧЕСКИМ РАБОТАМ

ПО ДИСЦИПЛИНЕ

«Дискретная математика»

Караганда 2010

Министерство образования и науки Республики Казахстан

Карагандинский государственный технический университет

Кафедра Вычислительной техники и программного обеспечения

А.В. Олейникова

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ПРАКТИЧЕСКИМ РАБОТАМ

ПО ДИСЦИПЛИНЕ

«Дискретная математика»

для студентов специальности

5В070400 «Вычислительная техника и программное обеспечение»

Караганда 2010

УДК 519.1(07)

ББК 22.176

М54

О - 53

А.В. Олейникова.Методические указания к практическим работам по дисциплине «Дискретная математика». Караганда: КарГТУ, 2010. 23с.

Методические указания к практическим работам составлены в соответствии с требованиями учебного плана и программы дисциплины «Дискретная математика». Методические указания включают в себя все необходимые сведения по выполнению тем практических работ курса и предназначена для студентов специальности 5В070400 «Вычислительная техника и программное обеспечение».

Рецензент – член редакционно-издательского совета КарГТУ И.В. Брейдо, д.т.н., профессор, зав. кафедрой АПП

Утверждено редакционно-издательским советом университета

© Карагандинский государственный технический университет, 2010

Содержание

Практическая работа № 1. Основные понятия теории множеств. Отношения……………………………………………………………………...…..4

Практическая работа № 2. Соответствия, отображения, функции. Взаимнооднозначные соответствия и мощности множеств. Теорема Кантора. Элементы теории нечетких множеств ………………………………….……......7

Практическая работа № 3 Элементы математической логики……………………………………….…………………………………......10

Практическая работа № 4 Исчисление высказываний и исчисление предикатов………………………………………………………………..……......15

Практическая работа № 5 Алгебраические структуры………………….…..…19

Практическая работа № 6 Элементы теории кодирования.…………….…...…19

Практическая работа № 7 Элементы комбинаторики..………………….…..…19

Практическая работа № 8 Теория графов………………….………………....…19

Практическая работа № 9 Числа графов. Поиск маршрутов в графе. Цепи и циклы………………………………………………………………………………19

Рекомендуемая литература………………………………………………....…...23

Практическая работа № 1.

Основные понятия теории множеств. Отношения.

Цель работы: Ознакомиться с понятием множества, с видами множеств и основными операциями над множествами. Изучить отношения

Порядок выполнения работы:

Практическая работа рассчитана на 2 часа аудиторных занятий, включающих в себя следующее:

1. Изучить:

- Понятие множества, способы задания множеств, виды множеств. Булеан множеств.

- Операции над множествами.

- Диаграммы Эйлера-Венна.

- Унарные, бинарные, тернарные отношения.

- Способы задания бинарных отношений и их основные свойства.

2. Выполнить каждый пункт упражнения согласно варианту. Номер индивидуального варианта задания определяется как сумма двух последних цифр зачётной книжки. Если значение суммы цифр превышает количества заданий, то значение суммы двух последних цифр зачетной книжки делится пополам. Если пункт упражнения не имеет подпункты, то в упражнении выполнить только пункт, соответствующий номеру варианта.

3. Оформить отчет о проделанной работе в соответствии с требованиями.

4. Проработать контрольные задания СРС.

Требования к отчету:

Отчет по практической работе распечатывается в виде твердой копии и состоит из следующих пунктов:

Вариант индивидуального задания;

Результаты полученных решений заданий;

Ответы на контрольные задания СРС.

Методические указания

Множеством называется совокупность каких-либо объектов, обладающим общим для всех характеристическим свойством. Это определение нельзя считать строгим, так как понятие множества является исходным понятием математики и не может быть определено через другие математические объекты. Один из основателей теории множеств Г. Кантор определял множество так: "Множество есть многое, мыслимое как целое".

Объекты, из которых состоят множества, называются их элементами.

Множества обозначают большими буквами, например А. В, С, а элементы – маленькими буквами, например, а, b, c.

Множество и его элементы обозначаются следующим образом:

А = {a1, a2, a3} – множество, состоящее из трех элементов;

А = {a1, a2, …} – множество, состоящее из бесконечного числа элементов.

Если элемент a принадлежит множеству А, это записывается следующим образом: a  А. Читается запись следующим образом: «элемент a принадлежит множеству А».

Если элемент a не принадлежит множеству А, то записывают так: a  А. Читается запись следующим образом: «элемент a не принадлежит множеству А».

Если все элементы множества А являются элементами множества В и наоборот, т. е. множества А и В совпадают, то говорят, что А = В.

Множество может содержать любое число элементов, конечное и бесконечное. Множество может содержать один элемент и ни одного.

Множество содержащее один элемент называется синглетоном.

Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается Æ.

Множества являются равными, если они состоят из одних и тех же элементов.

Например: {а,в,с} = {в,а,с}.

Если каждый элемент множества А является элементом множества В, говорят, что множество А является подмножеством множества В, и записывают А Í В или В Ê А. Отметим, что по определению само множество А является своим подмножеством, т.е. А Í А.

Если А Í В и В Í А, то по ранее введенному определению А = В.

Если А Í В и А ¹ В, то А есть собственное подмножество В, А Ì В. Если А не является собственным подмножеством В, то записывают А Ë В.

Пример: Пусть А – множество четных чисел, В – множество целых чисел, С – множество нечетных чисел. Тогда

А Ì В, С Ì В, А Ë С, В Ë А.

Не надо смешивать отношение принадлежности (Î) и отношение включения (Í).

Множество всех подмножеств множества Р называется булеаном множества Р и обозначается В(Р). Булеан множества Р={а,в,с}, имеет вид

В(Р)={ Æ, {с}, {b}, {b,с},{a},{a,с},{a,b},{a,b,с}}.

Для наглядного представления множеств и отношений между ними используется диаграммы Венна (иногда их называют кругами Эйлера или диаграммами Эйлера – Венна) в виде замкнутых кривых, ограничивающих области, которым ставятся в соответствие элементы тех или иных множеств. На рис.1 показано два множества:

Р={1,2,3,4,5,6} и К={1,2,3}. По диаграмме видно, что К Ì Р.

Множества не имеют общих элементов – изображаются непересекающимися кругами.

С

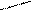K

Р В

Рис. 1

Универсальное множество (иногда используется термин «полное множество») обозначается символом I. Множество I – это множество всех тех элементов, которые участвуют в данном рассуждении.

Универсальное множество изображают в виде прямоугольника, а множества, входящие в универсальное множество, – в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга.

На рис. 2 показан пример универсального множества

I = {0,1,2,3,4,5,6,7,8,9} и двух его подмножеств Р = {2} и Q = {2,3,5,7}, где

Р- множество четных простых чисел, а Q – множество всех простых чисел, меньше 10

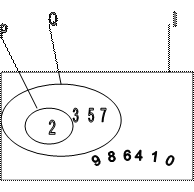
Рис. 2

С помощью диаграмм Венна удобно иллюстрировать операции над множествами.

Рисунок 1.1 – Круги Эйлера

Декартово произведение множеств

Рассмотрим два непересекающихся множества 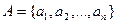и 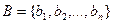. Выберем какой-нибудь элемент из множества А и припишем к нему справа некоторый элемент из множества В. Получим упорядоченную пару. Элементы, образующие пару, будем записывать в круглых скобках, отделяя один элемент от другого запятой: , где i = 1,2,3, … ,n; j= 1,2,3,…,m. Множество всех пар , называют декартовым произведением множеств. Для обозначения этой операции используется знак арифметического умножения АхВ.

Формально декартово произведение множеств А и В определяется следующим образом:

Читается эта запись так: декартово произведение множества А и В - это множество пар (x,y), где x – элемент множества А, y – элемент множества В.

Точно так же определяется декартово произведение множества B x A:

Рассмотрим пример. Пусть и В={a,b,c}, тогда

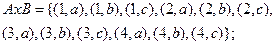
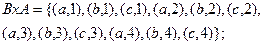
Из этих двух выражений следует, что , т.е. операция декартового произведения некоммуникативная.

Операция декартового произведения множеств ассоциативна

(АхВ)хС=Ах(ВхС)=АхВхС,

Для декартового произведения множеств справедливы следующие законы дистрибутивности.

Если |А| и |В| - кардинальные числа множества А и В, то

|АхВ|=|ВхА| =|А| 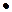|В|,

Где точка обозначает операцию арифметического умножения. Например, при А = {a,b,c}, B={1,2,3,4,5} имеем:

|A|=3; |B|=5; |AxB|=15

Если 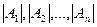- кардинальные числа множества то

=

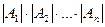
Понятие бинарного отношения

Пусть дано декартово произведение двух непустых множеств А и В, при этом множества могут быть любыми: непересекающимися, равными, входящими одно в другое и т.д. Элементами множества АхВ являются упорядоченные пары , где i = 1,2, … ,|A|; j= 1,2,…,|B|. Всякое подмножество декартова произведения АхВ называется бинарным отношением, определенным на паре множеств А и В. Для обозначения бинарного отношения принимают знак R. Поскольку R – это подмножество множества AxB, то можно записать 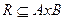. Если же требуется указать, что (а, b) 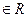, т.е. между элементами а и b 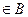,существует отношение R, то пишут aRb. Пусть напрмер:

А={1,2,3}; B={1,2,3,4,5,6} (24)

Множество АхВ содержит 18 упорядоченных пар. Выделим на этом множестве отношение «больше»: a>b, где а и b 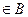, тогда

R = {(2,1),(3,1),(3,2)},

Многие авторы понятие бинарного отношения определяют через квадрат множества. Например, В.А. Горбатов пишет: «Бинарным отношением Т в множестве М называется подмножество его квадрата: »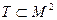

Задавать бинарные отношения можно различными способами. Наиболее употребительным является табличный способ. Его основу составляет прямоугольная система координат, где по одной оси откладываются элементы одного множества, по второй – другого. Пересечение координат образуют точки, обозначающие элементы декартового произведения. Бинарные отношения задаются двухмерными системами координат. Очевидно, что все элементы декартова произведения трех множеств могут быть представлены в трехмерной системе координат, четырёх множеств – в четырехмерной системе и т.д.

Второй способ представления отношений – в виде графов – применяется так же часто, как и первый (табличный). Способ задания отношений с помощью сечений используется реже.

Симметрия отношений

Пусть между элементами а 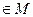и b 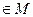имеется отношение R. Переставим местами a и b. Если при этом отношение R сохранится, то такое отношение симметричное.

Отношение является асимметричным, если оно имеет место между элементами a и b, но не отсутствует между элементами b и а.

Отношение является несимметричным в том случае, если оно не является симметричным, т.е. если имеет место отношение aRb, то отношение bRa может быть, но может и не быть.

Кроме симметричных, асимметричных, несимметричных отношений в математической литературе рассматриваются еще один вид симметрии – антисимметричность. Если отношения aRb и bRa имеют место лишь при a=b, то отношение R называют антисимметричным.

Транзитивность отношений

Любое отношение R в множестве М является либо транзитивным, либо интранзитивным ,либо не транзитивным.

Отношение R в множестве М называется транзитивным, если из aRb и bRc следует aRc.

Отношение называется интранзитивным, если из аRb и bRc следует, что утверждение aRc является ложным.

Отношение называется нетранзитивным, если оно не является транзитивным и не является интранзитивным, т.е. из того что имеет место отношение aRb и bRc, утверждение aRc может быть и истинным, и ложным.

Рефлексивность отношений

Отношение R в множестве М называется рефлексивным, если ни один элемент а 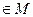утверждение aRa является истинным.

Отношения называются антирефлексивными, если ни один элемент а 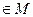не находится в отношении R с самим собой, такие отношения называются иррефлексивными).

Существуют отношения не являющиеся не рефлексивными, ни антирефлексивными. Пусть, например, М – множество точек на плоскости. Рассмотрим отношение: «точка а симметрична точке b относительно прямой, лежащей в той же плоскости». Если точки лежат не на прямой, то утверждения аRа и bRb являются ложными. Но все точки, лежащие на прямой, симметричны сами по себе. Следовательно, данное отношение не является рефлексивным и не является антирефлексивным.

Отношения эквивалентности

Если отношение R в множестве М обладает свойствами рефлексивности, симметричности и транзитивности, то оно называется отношением эквивалентности.

Отношения строгого порядка

Если отношение R в множестве М является транзитивным и ассиметричным и не является рефлексивным, то оно называется отношением строгого порядка. Пусть например, М = {1,2,3,4}. Тогда отношение «а больше b» имеет вид:

R = {(2,1),(3,1),(4,1),(3,2),(4,2),(4,3)}

Отношения не строгого порядка

Если отношение R в множестве М рефлексивно, антисимметрично и транзитивно, то оно называется отношением нестрогого порядка (используются так же термины: «отношение частичного порядка», «отношение квазипорядка», «отношение не полного порядка»).

Упражнения для выполнения:

Выполнить каждый пункт упражнения согласно варианту. Номер индивидуального варианта задания определяется как сумма двух последних цифр зачётной книжки. Если значение суммы цифр превышает количества заданий в упражнении, то значение суммы двух последних цифр зачетной книжки делится пополам. Упражнения не имеющие подпункты, выполняются не зависимо от варианта.

Дата добавления: 2015-07-26; просмотров: 1078; Нарушение авторских прав

Мы поможем в написании ваших работ!