Элементы теории кодирования

Цель работы: Ознакомиться представление о кодировании, расстоянии Хемминга, матричное кодирование и групповые коды.

Порядок выполнения работы:

Практическая работа рассчитана на 2 часа аудиторных занятий, включающих в себя следующее:

1. Изучить:

- Представление о кодировании.

- Расстояние Хемминга.

- Теорема о корректирующей способности кодов.

- Матричное кодирование.

- Групповые коды.

- Коды Хемминга

2. Решить упражнения к данному разделу. Выполнить каждый пункт упражнения согласно варианту. Вариант определяется как сумма двух последних цифр зачётной книжки, если количество заданий в пункте упражнения меньше, чем полученная цифра, то эта цифра делится пополам (берётся её целая часть).

3. Оформить отчет о проделанной работе в соответствии с требованиями.

4. Проработать контрольные задания СРС.

Требования к отчету:

Отчет по практической работе распечатывается в виде твердой копии и состоит из следующих пунктов:

Вариант индивидуального задания;

Результаты полученных решений заданий;

Ответы на контрольные задания СРС.

Методические указания

Передача информации сводится к передаче по некоторому каналу связи символов некоторого алфавита. Для обеспечения надёжности передачи информации в таких системах разработаны эффективные методы, использующие коды различных типов.

Рассмотрим одну из таких моделей, связанную с групповыми кодами.

Алфавит в котором в котором записываются сообщения, считаем состоящим из двух символов [0;1]. Он называется двоичным алфавитом. Тогда сообщение есть конечная последовательность символов этого алфавита.

Сообщения подлежащие передаче, кодируются по определенной схеме, более длинной последовательностью символов в алфавите [0;1]. Эта последовательность называется кодом или кодовым словом.

При приёме можно исправлять или распознавать ошибки, возникшие при передаче по каналу связи, анализируя информацию, содержащуюся в дополнительных символах. Принятая последовательность символов декодируется по определённой схеме в сообщение, с большой вероятностью совпадающее с переданным.

Блочный двоичный (m,n)-код определяется двумя функциями:

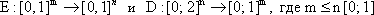- множество всех двоичных последовательностей длины n.

Функция Е определяет схему кодирования, а функция D-схему декодирования. Математическую модель системы связи можно представить в виде схемы:

Здесь Т - "функция ошибок", Е и D выбираются таким образом, чтобы композиция DoToE была функцией, с большой вероятностью близкой к тождественной. Двоичный (m,n)-код содержит 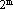кодовых слов.

На множестве двоичных слов длины m расстоянием d(a,b) между словами а и b называют число несовпадающих позиций этих слов, например: расстояние между словами a=01101 и b=0011 равно 3.

Определённое таким образом понятие называется расстоянием Хемминга. Оно удовлетворяет следующим аксиомам расстояния:

1) d(a,b) 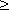0 и d(a,b)=0 тогда и только тогда когда a=b

2) d(a,b)=d(b,a)

3) d(a,b)+d(b,c) 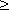d(a,c) (неравенство треугольника)

Весом w(a) слова a называют число единиц среди его координат.

Расстояние между словами a и b есть вес их суммы a b: d(a,b)=w(a b), где символом обозначена операция покоординатного сложения по модулю 2.

Теорема 1. Для того чтобы код позволял обнаруживать ошибки в k (или менее) позициях, необходимо и достаточно, чтобы наименьшее расстояние между кодовыми словами было k+1.

Теорема 2. Для того чтобы код позволял исправлять все ошибки в k (или менее) позициях, необходимо и достаточно, чтобы наименьшее расстояние между кодовыми силами было 2k+1.

Пусть G= 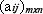- матрица порядка mxn с элементами , равными 0 или 1. Символ обозначает сложение по модулю 2. Тогда схема кодирования задаётся системой уравнений или в первичной форме b=aG, где а=(а , а ... а ) - вектор, соответствующий передаваемому сообщению; b==(b , b ... b )- вектор соответствующий кодированному сообщению; G - порождающая матрица кода.

Порождающая и проверочная матрицы

Пусть С двоичный линейный (n, k, d_min) код. Так как С есть k-мерное подпространство, то оно имеет базис, например, (v₀, v₁,..., v_k-1) такой, что любое кодовое слово v Î С может быть записано как линейная комбинация элементов этого базиса:

v = u₀v₀ + u₁v₁ + … + u_k-1v_k-1,

где u_i Î {0, 1}, 0 £ i <k. Уравнение (7.11) может быть записано в матричной форме через порождающую матрицу G и вектор-сообщение u = (и₀, и₁,..., и_k-1): ,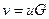

где

Так как С является k-мерным векторным пространством в V₂, то существует (n-к)-мерное дуальное пространство {dual space) C^{^}, которое порождается строками матрицы Н, называемой проверочной матрицей {parity-check matrix), такой, что GH^T=0, где через Н^T обозначена транспонированная матрица Н. Заметим, в частности, что любое кодовое слово v Î С удовлетворяет условию

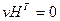, уравнение является фундаментальным для декодирования линейных кодов.

Линейный код С^{^}, который генерируется матрицей Н, является двоичным линейным (п, п–k, 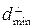) кодом, который называют обычно дуальным коду С.

Если кодирование должно быть систематическим, то произвольная порождающая матрица G линейного блокового (n, k, d_min) кода С может быть преобразована к систематической форме G_sys (иначе, к канонической форме) с помощью элементарных операций и перестановок столбцов матрицы. Матрица G_sys состоит из двух подматриц: k x к единичной матрицы, обозначаемой I_k, и k х (п - k) проверочной подматрицы Р. Таким образом,

,

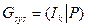где

)

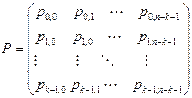Так как GH^T = 0, то отсюда следует, что систематическая форма проверочной матрицы имеет вид

.

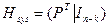Упражнения для выполнения:

1. Организовать передачу кодовой комбинации 1100 с использованием кода Хемминга. Число проверочных разрядов n-k=3. В коде Хемминга они разместятся на первом a1, втором a2, на четвертом a4 местах.

2. Организовать передачу кодовой комбинации 1011 с использованием кода Хемминга. Число проверочных разрядов r=3. Кодовая комбинация имеет вид a1a2 1 a4 0 1 1

3. Организовать передачу кода 01001010 с использованием кода Хемминга.

4. Организовать передачу кода X=10101010 с использованием кода Хемминга.

5. Запишем совокупность комбинаций, получающуюся циклическим сдвигом комбинации 001011

Контрольные задания для СРС

Дайте определение расстояния Хэмминга.

Опишите процесс матричного кодирования.

Сформулируйте теорему о корректирующей способности кодов.

Дата добавления: 2015-07-26; просмотров: 389; Нарушение авторских прав

Мы поможем в написании ваших работ!