
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Унимодальные и выпуклые функции
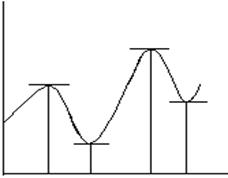
В практике решения оптимизационных задач встречаются случаи, когда нужно исследовать одномерные целевые функции. При этом особую роль играют значения аргументов х, отделяющие интервал возрастные функции от интервала убывания и наоборот. В этих точках целевая функция F(x) меняет характер своего поведения. Если имеет место случай F1 ~ х1, т.е. точка х1 отделяет интервал возрастания от интервала убывания, то существует такая окрестность точки х1, что значение функции F1(x1) является наибольшим в этой окрестности. В противном случае, например, точка х2 имеет место наименьшее значение функции F2(x2) в окрестности точки х2. Сказанное можно геометрически проиллюстрировать следующим рисунком.
F
 x
x
x1 x2 x3 x4
Рис. 1. Многоэкстремальная функция
Точка х0 называется точкой максимума F(x), если F(x0) есть наибольшее значение функции F(x) в окрестности точки х0. И по аналогии, точка х0 называется точкой минимума, если F(x0) есть наименьшее значение F(x) в окрестности х0. Точки максимума и минимума объединяются общим названием экстремум.
При этом в теории оптимизации различают понятия локальные и глобальные экстремумы. Так, на рис.5. изображена произвольная целевая функция, содержащая два локальных и один глобальный минимумы.
Q (x)
 x
x
Рис. 2. Произвольная одномерная функция
Общим для всех типов оптимизационных задач является то, что в зависимости от числа варьируемых переменных функции могут быть одномерными (n=1) или многопараметрическими. В первом случае осуществляется поиск минимума произвольной кривой Q(x), во втором осуществляется минимизация некоторой n-мерной гиперповерхности.
Точка х* называется точкой локального (относительного) минимума, если для всех точек х, принадлежащих ε - окрестности d(х* ε) этой точки, значение Q(x) не принимает меньшего значения:
Q(x*)≤Q(x) для всех хЄD, то есть глобальный минимум — это наименьший из всех локальных.
Простейшим из нелинейных функций являются выпуклые функции. Геометрически это свойство означает, что функция Q(x) расположена ниже любой прямой, соединяющей две точки на её поверхности. Например, на рис.6. множество А будет выпуклым, а множество В таковым не является.
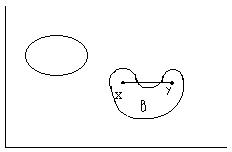
Рис. 3. Примеры выпуклых и невыпуклых множеств
При этом под множеством будем понимать арифметическое n-мерное пространство Rn элементами которого являются упорядоченные наборы из n вещественных чисел x=(x1, x2, x3…, xn). Указанные элементы будем называть точками или векторами, не различая этих понятий, а соответствующие им числа — координатами точки или компонентами вектора.
С выпуклыми множествами мы уже встречались в предыдущем разделе, когда рассматривали в теории решений множество стратегий.
Более общий класс нелинейных функций, т.е. функции имеющие единственный локальный минимум в области D, который будет в этом случае глобальным. Геометрически условие унимодальности сводится к следующему требованию:
Необходимо, чтобы для любых точек x ≠ x* существовал строго падающий путь на поверхности Q(x), ведущий от x до x*.
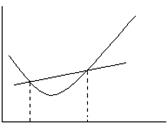
На рис.7. приведены некоторые примеры унимодальных одномерных функций.
 x
x
x1 x2 x1 x2
Рис. 4. Одномерные унимодальные функции
Функции, имеющие несколько локальных минимумов, будем называть многоэкстремальными функциями.
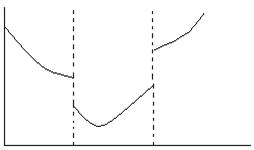
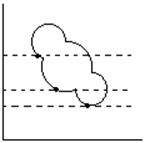
В задачах нелинейного программирования тип оптимального решения x* (будет ли x* локальным или глобальным минимумом) зависит не только от вида функции Q(x), но и от того, является ли допустимая область управляемых переменных D выпуклым множеством. Для выпуклой функции (рис.6 а) и выпуклого множества D локальный минимум является в тоже время и глобальным. Для не выпуклой области D даже при выпуклой функции задача не линейного программирования может оказаться многоэкстремальной, т.е. иметь несколько локальных минимумов (рис.8.)
x2
 x1
x1
Рис. 5. Пример многоэкстремальной функции
Локальные (А,В) и глобальные (С) минимумы функции Q(x) = x2, определенной на невыпуклом множестве D.
Необходимый признак экстремума
Если в точке х0 функция Q(x) достигает экстремума, то ее производная в этой точке либо равна нулю, либо не существует. Этот признак полностью согласуется с теоремой Ферма: если непрерывная функция в некотором интервале (х1, х2) принимает свое наибольшее (наименьшее) значение во внутренней точке этого интервала х1<ε<х2 и она дифференцируема, то она обязательно равна нулю. С геометрической точки зрения рассматриваемый признак означает, что касательная к графику функции в его вершине параллельна оси ох (рис. 4). Важно подчеркнуть, что необходимый признак экстремума не является достаточным, т.е. из того, что производная в данной точке обращается в нуль ( или ее не существует), еще не следует, что эта точка будет точкой экстремума. В утверждение этого тезиса приведем графический пример.
Y(х) Y = x3

Y(х) Y = 3√x
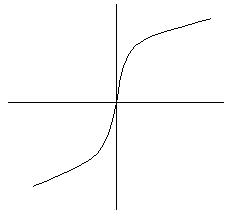
Рис. 6. Примеры функций, не имеющих экстремума
Так, функция y=x3 имеет производную y’=3x2, обращающаяся в нуль при x=0.Однако точка x=0 вовсе не является точкой экстремума. Функция y= 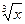 ,для которой y'=1/3
,для которой y'=1/3 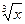 2 не имеет смысла при x=0. И в последнем случае точка x=0 не является экстремальной.
2 не имеет смысла при x=0. И в последнем случае точка x=0 не является экстремальной.
Первый признак достаточности экстремума
Точка x0 является точкой экстремума функции f(x) ,если производная f’(x) при переходе через x0 меняет знак на противоположный; при перемене знака “+” на “-“ точка x0 является точкой максимума; при противоположной смене знаков- соответственно точкой минимума.
Следует заметить,что основываясь только на перемене знака производной, нельзя однозначно говорить о наличии экстремума. Необходимо еще убедиться в том ,что в самой тоже функция непрерывна.
 Производная этой функции y’=-
Производная этой функции y’=- 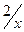 3 меняет знак при переходе через точку x=0; слева от нее y’
3 меняет знак при переходе через точку x=0; слева от нее y’  0 и, значит функция возрастает, справа от нуля y’
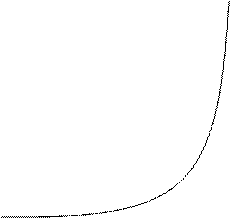
0 и, значит функция возрастает, справа от нуля y’  0 и, значит функция убывает; сама же точка x=0 не является экстремальной, т.к. функция в ней имеет бесконечный разрыв. Очевидность этих рассуждений иллюстрируется рис.10.
0 и, значит функция убывает; сама же точка x=0 не является экстремальной, т.к. функция в ней имеет бесконечный разрыв. Очевидность этих рассуждений иллюстрируется рис.10.
У 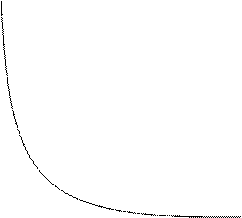
 |



0 х
Рис.7. График функции y= 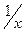 2
2
Второй признак достаточности экстремума
Точка x0 есть точка экстремума функции f(x), если f’(x0)=0, а f’’(x0)  0,причем, если f’’(x0)
0,причем, если f’’(x0)  0, то x0-точка минимума.
0, то x0-точка минимума.
 По своей применимости второй признак достаточности оказывается весьма удобным: вместо рассмотрения функции f’(x) в точках, отличных от предполагаемой точки экстремума, он позволяет дать ответ по знаку функции f’’(x) в той же точке.
По своей применимости второй признак достаточности оказывается весьма удобным: вместо рассмотрения функции f’(x) в точках, отличных от предполагаемой точки экстремума, он позволяет дать ответ по знаку функции f’’(x) в той же точке.
| <== предыдущая страница | | | следующая страница ==> |
| Параметрическая транспортная задача | | | Прямые методы поиска оптимального решения |
Дата добавления: 2015-07-26; просмотров: 242; Нарушение авторских прав

Мы поможем в написании ваших работ!