Прямые методы поиска оптимального решения

Терминологически этот класс методов имеет различные названия: метод сканирования, метод перебора, метод итерации или шаговый поиск, методы безусловного экстремума. В свою очередь, методы поиска безусловного экстремума могут быть разделены на методы минимизации (максимизации) унимодальных функций и методы глобальной минимизации многоэкстремальных функций.

По способу получения информации о расположении точки испытания (очередная итерация) на каждом шаге методы поиска можно разделить на детерминированные методы и методы случайного поиска.

По определению способа очередной точки методы подразделяются на методы последовательного поиска и методы пассивного поиска. Методы последовательного поиска указывают очередную точку, в которой вычисляется целевая функция. Q(x) на основании данных, полученных на предыдущем шаге. Методы пассивного поиска указывают все точки одновременно (до первого вычисления функции Q(x)).

Прямые методы поиска оптимального решения предполагают, вообще говоря, последовательное пошаговое вычисление критерия оптимизации и ограничений при фиксированных значениях параметров x=(x₁,x₂,…,x_n) и варьировании параметра x_n. Такой алгоритм может потребовать больших затрат машинного времени. В связи с этим возникает проблема решения задачи при наименьшем числе испытаний. Путь ее решения лежит на использовании рекуррентных соотношений, которые для начального приближения x₀ в общем виде можно записать следующим образом

x^r=F_r[x⁰,Q(x⁰),g(x⁰);…;x^r-1,Q(x^r-1),g(x^r-1)], (4)

r= .

После проведения N испытаний (итераций, шагов поиска), связанных с определением из (6) векторов x², приближенное значение функции критерия Q^* выбирается из условия

Q^*=Q(x^*)=minQ(x^r) (5)

0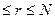

Выражение (7) и начальное приближение x⁰ вместе с системой соотношений (8) являются математической записью метода поисковой оптимизации.

При отсутствии ограничений g(x) соотношение (7) прямой вид x^r=F_r[x⁰,Q(x⁰);…;x^r-1,Q(x^r-1)] (3), который и определяет группу методов поиска безусловного минимума.

Если в соотношениях (1) и (2) вместо вектора x^r рассматривается скалярная величина, то методы поиска называются одномерными. В противном случае - многопараметрическими.

Методы поиска безусловного минимума (как одномерные, так и многопараметрические), в свою очередь, могут быть разделены на методы минимизации унимодальных функций и методы минимизации экстремальных функций.

Рассмотрим метод поиска оптимального решения на примере одномерной минимизации унимодальной функции.

Пусть требуется найти минимум одномерной функции min Q(x) x 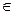D,где D={x:a 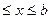}(1).

Функция Q(x) принадлежит классу унимодальных функций, т.е. существует значение x^* ,такое, что Q(x) строго убывает при x x^* и строго возрастает при x x^*. При помощи фиксированного числа шагов (испытаний) N,которые могут быть проведены в любой тоже интервала [a,b], требуется локализовать положение минимума x^* с небольшой точностью. Для решения этой задачи в условиях, когда положение x^* возможен только один путь- сокращение интервала неопределенности.

Стратегия проведения испытаний строится таким образом, чтобы в процессе поиска происходило исключение тех подинтервалов, в которых в силу унимодальности функции Q(x) точное x^* отсутствует. Это позволяет после проведения N испытаний выделить некоторый подинтервал, принадлежащий отрезку [a,b] и содержащий точку x^*.

Сокращение интервала неопределенности осуществляется на основе так называемого “наилучшего алгоритма поиска”, под которым понимается алгоритм, для которого интервал неопределенности имеет наименьшее значение, т.е.

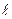^*_n= 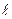_n(F^*)=min max 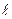_n(Q,Fⁱ) Fⁱ 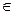A_F Q 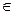K_Q (6)

Отсюда следует, что величина интервала неопределенности зависит от алгоритма поиска F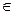^* A_F^*, от вида функции Q(x) 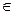K_Q, определяющей конкретный индекс k, при котором получено минимальное ее значение.

Наиболее простыми алгоритмами поисковой оптимизации являются алгоритмы, реализующие F¹₁- метод равномерного поиска и F₁²- метод равномерного дихотомического поиска. В них расположение точек xⁱ выбирается заранее до проведения первого испытания, т.е. шаги распределяются равномерно на всем интервале [a,b]. В полученных точках оцениваются значение функции Q(x) и из них выбирается наименьшее. В методе дихотомического поиска шаги выбираются также равномерно, но значение функции оценивается парой подинтервалов. Недостатком этих алгоритмов является то, что в них при выборе точек x_i не используется информация, полученная в x_i-1 шаге. Этот недостаток устранен в методе деления пополам и в методе последовательного дихотомического поиска.

В методе деления пополам координаты каждой последующей пары шагов выбираются в средней точке текущего интервала неопределенности. По значениям функции Q(x) полученным в этих точках, одна половина исследуемого интервала исключается из дальнейшего рассмотрения в силу унимодальности исследуемой функции. В середине оставшейся части интервала вновь делается пара испытаний и т.д. Среди прямых методов поиска оптимального решения необходимо выделить градиентные методы наискорейшего спуска.

Общая схема решения задач данным методом стоит в построении последовательности x₀,x₁,x₂,…,x_n,…решений по следующему принципу: в качестве x₀ выбирается, вообще говоря, любая точка области решений и затем каждая последующая точка получается из предыдущей по формуле (7) x_k+1=x_k+ 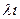, где ₁, ₂,…, _n) некоторое направление (вектор), а 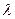-действительное число. При этом направление и длина шага выбирается так, чтобы обеспечить сходимость процесса оптимального решения x^*.

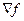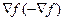Так как направление градиента целевой функции является направлением ее наискорейшего роста, то при отыскании max вогнутой функции (минимума вогнутой функции) в качестве часть берется и тогда формула принимает вид

X_k+1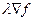=x_k+ (x_k), 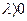- если имеется максимум, и

X_k+1=x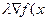_k- _k), 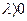- если ищется минимум. (7)

Методы спуска, в которых итерационная последовательность x₀, x₁, x₂,…, x_k…находится по формулам (8) называются градиентными. Эти методы отличаются друг от друга способами выбора длины шага и алгоритмами нахождения точки x_k+1, которые изложены выше.

Выбор длины шага очень важен, т.к. при его нерациональной величине можно “проскочить” искомый экстремум.

Определение.Если величина шага 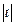= 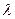выбирается так, чтобы приращение функции 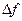при перемещении из предыдущей точки в последущую было наибольшим (при f_max) или наименьшим (при f_min), то градиентный метод называется методом наискорейшего спуска.

Для случая функции двух переменных f(x,y) метод наискорейшего спуска имеет простую геометрическую интеграцию:

для любого k_i луч, идущий от точки x_k к точке x_k+1 перпендикулярен к линии уровня функции f(x,y), проходящей через точку x_k (т.к. направлен по градиенту), и касается линии уровня, проходящей через точку x_k+1.

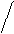
F

X^*

X₁ x₃ x₄

X₂

X₀

X

Рис. 8. Линии уровня f (x,y)= const

Отличие этих методов заключается в том, что в методе градиентного спуска величина шага постоянна для каждой итерации, а для метода наискорейшего спуска характерен переменный шаг.

Дата добавления: 2015-07-26; просмотров: 240; Нарушение авторских прав

Мы поможем в написании ваших работ!