
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Методы, использующие производные целевой функции
 Схема исследования функций на экстремумы должна содержать последовательность действий для изучения роста и отыскания экстремумов непрерывной функции f(x) в заданном интервале, который может быть нам конечным, так и бесконечным. Для определенности будем считать, что функция y=f(x) имеет производную всюду, за исключением, может быть, отдельных точек. Алгоритм исследования содержит следующие процедуры.
Схема исследования функций на экстремумы должна содержать последовательность действий для изучения роста и отыскания экстремумов непрерывной функции f(x) в заданном интервале, который может быть нам конечным, так и бесконечным. Для определенности будем считать, что функция y=f(x) имеет производную всюду, за исключением, может быть, отдельных точек. Алгоритм исследования содержит следующие процедуры.
 1. Прежде всего, нужно найти точки интервала, в которых производная равна нулю (стандартные точки), т.е. действительные корни уравнения f’(x)=0, а также те точки, в которых производная не существует. Обозначим все найденные точки в порядке возрастания через x1, x2,…., xn.Таким образом, x1
1. Прежде всего, нужно найти точки интервала, в которых производная равна нулю (стандартные точки), т.е. действительные корни уравнения f’(x)=0, а также те точки, в которых производная не существует. Обозначим все найденные точки в порядке возрастания через x1, x2,…., xn.Таким образом, x1  x2
x2  …
…  xn .Это те точки интервала, в которых функция f(x) может иметь экстремумы. Иногда их называют критическими.
xn .Это те точки интервала, в которых функция f(x) может иметь экстремумы. Иногда их называют критическими.
 2. Затем разбиваем при помощи точек xi весь заданный интервал [a;b] на частные интервалы: (a,x1),(x1,x2)…,(xn-1,xn),(xn,b), в каждом из которых производная сохраняет постоянный знак. Это операция носит название- проверка монотонности функции интервала.
2. Затем разбиваем при помощи точек xi весь заданный интервал [a;b] на частные интервалы: (a,x1),(x1,x2)…,(xn-1,xn),(xn,b), в каждом из которых производная сохраняет постоянный знак. Это операция носит название- проверка монотонности функции интервала.
 3. Находим знак производной в каждом из частных интервалов, для чего достаточно узнать ее знак в какой-нибудь одной точке интервала. По знаку производной определяем характер изменения функции в каждом интервале монотонности, т.е. возрастание или убывание. Следя за знаком производной при переходе через границы интервалов монотонности, выясняем, какие из этих точек будут точками max или min.
3. Находим знак производной в каждом из частных интервалов, для чего достаточно узнать ее знак в какой-нибудь одной точке интервала. По знаку производной определяем характер изменения функции в каждом интервале монотонности, т.е. возрастание или убывание. Следя за знаком производной при переходе через границы интервалов монотонности, выясняем, какие из этих точек будут точками max или min.
 4. Подстановкой в выражение функции f(x) критических значений x=xi находим соответствующее значение функции f(x1), f(x2),…,f(xn). Как уже отмечалось, не всегда эти функции могут иметь экстремальное значение (рис.9).
4. Подстановкой в выражение функции f(x) критических значений x=xi находим соответствующее значение функции f(x1), f(x2),…,f(xn). Как уже отмечалось, не всегда эти функции могут иметь экстремальное значение (рис.9).
 Результаты исследований целесообразно свести в таблицу (1).
Результаты исследований целесообразно свести в таблицу (1).
Таблица 1
| x | a | a  x x  x1 x1
| X1 | X1  x x  x2 x2
| X2 | X2  x x  b b
| b |
| y | f(a) | возрастает | f(x1) | убывает | f(x2) | убывает | (b) |
| y’ | + | - | - |
Для примера рассмотрим функцию y=3x3+4.5x2-4x+1.
Эта функция имеет непрерывную производную на всей оси x..
Находим производную y’=9x2+9x-4=(3x-1)(3x+4).Отсюда видно, что производная равна нулю при x= 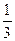 и x=-
и x=- 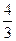 .Так как при x
.Так как при x  -
- 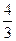 оба сомножителя отрицательны, то производная при этих значениях x положительна и, следовательно, функция возрастает. При -
оба сомножителя отрицательны, то производная при этих значениях x положительна и, следовательно, функция возрастает. При - 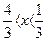 производная отрицательна- функция убывает, а при x
производная отрицательна- функция убывает, а при x 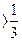 производная снова положительна и функция возрастает. Таким образом, x=-
производная снова положительна и функция возрастает. Таким образом, x=- 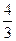 есть точка максимума, а x=
есть точка максимума, а x= 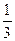 -точка минимума и мы имеем три интервала монотонности: от -∞ до -
-точка минимума и мы имеем три интервала монотонности: от -∞ до - 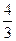 -интервал возрастания, от -
-интервал возрастания, от - 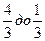 - интервал убывания и от
- интервал убывания и от 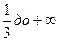 - интервал возрастания. Вычислим значения функции в точках экстремума и составим таблицу поведения функции:
- интервал возрастания. Вычислим значения функции в точках экстремума и составим таблицу поведения функции:
Таблица 2
| x | - 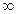
| - 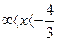
| 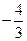
| 
| 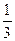
| 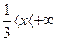
| 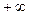
|
| y | 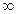
| возрастает | 7  max max
| убывает | 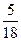 min min
| возрастает | 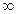
|
| y’ | - 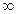
| + | - | + |
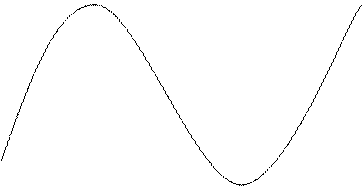
По таблице можно составить график
 Y
Y
- 7
 - 6
- 6
- 5
- 4
- 3
- 2
 - 1
- 1  x
x
- 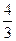 -1 0
-1 0 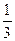 1
1
Рис. 9. График функции y=3x3+4.5x2-4x+1
Описанная выше схема исследования функции и алгоритм вычислений представляет собой типичный метод, использующий производные целевой функции. Эти методы являются предпосылкой для рассмотрения прямых методов оптимизации.
| <== предыдущая страница | | | следующая страница ==> |
| Прямые методы поиска оптимального решения | | | Многомерная оптимизация без ограничений |
Дата добавления: 2015-07-26; просмотров: 149; Нарушение авторских прав

Мы поможем в написании ваших работ!