Принцип оптимальности и уравнения Беллмана

Принцип оптимальности по Беллману означает: каково бы ни было состояние системы, полученное в результате какого-либо числа шагов, на ближайшем шаге нужно выбрать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.

Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом.

Графически этот процесс выглядит следующим образом:

- условно оптимальный выигрыш на n-м шаге или условный МАХ целевой функции

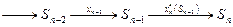
-n-й шаг

f_n-1(S_n-2,X_n-1)– значение целевой функции на n-1м шаге

Рис. 23. Вид процесса без обратной связи

На этом рисунке:

S_n-2 – состояние системы к началу n-1 шага,

X_n-1 – управление на n-1 шаге,

X_n^*(S_n-1) – условное оптимальное управление на n-ом шаге.

Рассмотрим n-ый шаг:

S_n-1 – состояние системы к началу n-го шага,

S_n=S^ - конечное состояние системы,

X_n – управление на n-ом шаге,

f_n (S_n-1,X_n) – целевая функция (выигрыш) n-го шага.

Согласно принципу оптимальности X_n нужно выбрать так, чтобы для любых состояний S_n-1 получить максимум целевой функции на этом шаге, тогда,

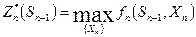(16)

уравнение Беллмана для одномерной задачи оптимизации, т.е. Z_n^* и есть условный максимум целевой функции на n-ом шаге. Максимизация ведется по всем допустимым управлениям X_n.

Решение X_n, при котором достигается Z_n^* (S_n-1), также зависит от S_n-1 и называется условным оптимальным управлением на n-ом шаге и обозначается через X_n^*(S_n-1). Решив одномерную задачу локальной оптимизации по уравнению (*), можно найти для всех возможных состояний (S_n-1) две функции: Z_n^* (S_n-1) и X_n^*(S_n-1) целевую и управления соответственно.

Рассмотрим теперь двухшаговую задачу, для чего к n-му шагу присоединим n-1 шаг. Тогда по определению для любых состояний S_n-2, произвольных управлений X_n-1 и оптимальном управлении на n-ом шаге значение целевой функции на двух последних шагах равно:

f_n-1(S_n-2,X_n-1) + Z_n^*(S_n-1) (17)

В соответствии с принципом оптимальности решение нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем n-ом шаге приводило бы к максимуму целевой функции на двух последних шагах.

Нужно найти max выражения (1) по всем допустимым управлениям на (n-1) шаге.

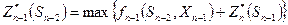(18)

Это и есть уравнение оптимальности для двухшагового управления. В общем виде уравнение Беллмана выглядит так:

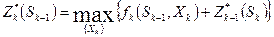, (19)

где - условный максимум целевой функции при оптимальном управлении на k-м шаге

k=n-1, n-2,…, 2, 1

- условное оптимальное управление на k-м шаге

Таким образом, в результате условной оптимизации получаются две последовательности:

Z_n^* (S_n-1), Z_n-2^*(S_n-2),…, Z₂^*(S₁), Z₁^*(S₀) – условные максимумы целевой функции на последнем, на двух последних, на n шагах и X_n^*(S_n-1), X_n-1^*(S_n-2),…, X₂^*(S₁), X₁^*(S₀) – условные оптимальные управления на n-м, n-1-м,…, втором и первом шагах.

Использование перечисленных методов математического программирования позволяет и оптимально отнестись к планированию деятельности организации.

Дата добавления: 2015-07-26; просмотров: 154; Нарушение авторских прав

Мы поможем в написании ваших работ!