Краткие сведения из векторной алгебры

Пусть в области G пространства задана функция u =f (P) (P – любая точка области). Это означает, что в области G определено скалярное поле. Если G – область трехмерного пространства, то скалярное поле u можно рассматривать как функцию трех переменных x, y, и z (координат точки Р):

u = u (x, y, z). (5.10)

Пусть эта функция однозначна и имеет непрерывные частные производные первого порядка. При переходе из одной точки пространства к другой функция изменяется с некоторой скоростью. В каком-то направлении эта скорость будет максимальна, и называется градиентом функции. Градиент – величина векторная:

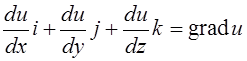, (5.11)

где i, j, k - единичные векторы (орты)

Итак, градиент есть вектор, направленный по нормали к поверхности уровня в сторону возрастания и численно равна скорости изменения функции по этому направлению.

Для сокращения записей в векторной алгебре вводится понятие формального символического вектора .– оператора Гамильтона ( - набла):

. (5.12)

В этом случае градиент трактуется как произведение оператора Гамильтона на скалярную функцию

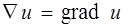. (5.13)

Рассмотрим векторную функцию 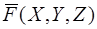, заданную своими проекциями. Определим скалярное произведение вектора 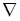и вектора :

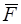. (5.14)

В результате получается скалярная функция – дивергенция вектора 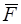. Дивергенция характеризует расходимость или мощность источника.

Возьмем векторное произведение вектора 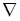и вектора 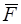При этом будем иметь в виду, что jx k = i , иi*i = 0 .

. (5.15)

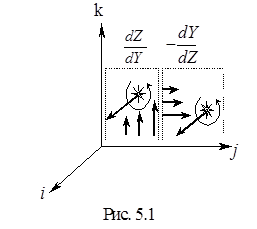Получился новый вектор, который характеризует вращательную способность вектора F. Рассмотрим одну координату ротора. Первая составляющая ( ) – есть скорость изменения координаты Z самого вектора в направлении орты j. В этом направлении вектор растет, и как бы закручивает мельницу против часовой стрелки (рис. 5.1). Плоскость кручения обозначается стрелкой, перпендикулярной к плоскости, направленной к зрителю, и в данном случае по направлению оси i. Вторая составляющая – скорость изменения координаты Y самого вектора в направлении орты к. Стрелка кручения так же направлена по оси i. Остальные координаты ротора получаются таким же образом.

Дата добавления: 2015-07-26; просмотров: 168; Нарушение авторских прав

Мы поможем в написании ваших работ!