Скалярный магнитный потенциал

Согласно первому уравнению Максвелла в тех местах, где есть плотность тока, ротор вектора напряженности не равен нулю и поле имеет вихревой характер. В тех областях, где плотность тока равна нулю ( ) 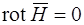, магнитное поле можно рассматривать как потенциальное. Каждая точка такой области будет иметь скалярный магнитный потенциал j_м . Следовательно, для таких областей можно принять

. (5.89)

Однако физической сути скалярный магнитный потенциал не имеет, и является величиной многозначной. Для однозначности необходимо, чтобы путь перемещения из одной точки в другую не проходил через контуры с током. Задача расчета магнитного поля при этом сводится к следующему:

· Определению потенциальной функции j_m(x,y,z);

· Нахождению значения напряженности (H).

Так как формально j_m полностью аналогична j электростатического поля, то для магнитного потенциала справедливо выражение:

, (5.90)

или 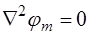. (5.91)

Это дифференциальное уравнение, имеющее бесчисленное множество решений. Единственное решение может быть найдено для конкретного случая с учетом граничных условий.

Дата добавления: 2015-07-26; просмотров: 256; Нарушение авторских прав

Мы поможем в написании ваших работ!