Тема 10. Преобразования КС-грамматик

План лекции

1. Преобразования КС-грамматик

2. Построение грамматики с продуктивными нетерминалами

Представление грамматики в виде графа Дерево грамматического разбора не следует путать с представлением грамматики в виде графа. Граф грамматики в качестве вершин содержит сентенциальные формы (любые цепочки, выводимые из аксиомы).

Рассмотрим представление грамматики G в виде графа: G = (VT, VN, Р, S), в которой VT =

{a, b, с}, VN = {S}, P={S → aSa | bSb | c}.

Преобразования КС-грамматикЧасто требуется изменить грамматику таким образом, чтобы она удовлетворяла определенным требованиям, не изменяя при этом порождаемый грамматикой язык. Для этого используются эквивалентные преобразования КС-грамматик, некоторые из которых рассмотрены ниже.

Удаление правил вида А → В

Преобразование первого типа состоит в удалении правил А → В, или <нетерминал> → <нетерминал>.

Покажем, что для любой КС-грамматики можно построить эквивалентную грамматику, не содержащую правил вида: А → В, где А и В - нетерминальные символы.

Пусть имеется КС-грамматика G=(V_T, V_N, P, S), где множество нетерминалов V_N={A₁, A₂, . . . , A_n}. Разобьем Р на два непересекающихся множества: P = P₁ È P₂. В P₁ включены все правила вида Аi → Ak, в P₂ включены все остальные правила, т.е. P₂ = P \ P₁. Затем для каждого А_i определим множество правил P(А_i), включив в него все такие правила А_i→ϕ, что А_i →* A_j и А_j → ϕ, где А_j → ϕ Î P₂. Построим эквивалентную КС-грамматику G_э = (V_T, V_N, P_э, S), в которой множества терминальных и нетерминальных символов, а также аксиома совпадают с теми же объектами исходной грамматики G, а множество правил P_э получено объединением правил множества P₂ и правил P(А_i) для всех 1≤ i ≤n:

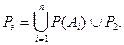
Пример. Пусть задана грамматика G со следующими правилами вывода S → aFb | А; А

→ аА | В; В → aSb | S; F → bc | bFc.

Построим множества правил Р2, P(S), P(A), P(B), P(F).

Определим правила для Р2: Р2 = {S → aFb; А → аА; В → aSb; F → bc | bFc}.

Определим правила для P(S): S => A => B или S =>*А; S=>В, где =>* обозначает непосредственную выводимость. P(S) = {S → аА; S → aSb).

Определим правила для Р(А): А => В => S или А =>* В; А => S. Р(А) = {А → aSb; А → aFb}.

Определим правила для Р(В): В => S => А или В =>* S; В =>*А. Р(В) = {В → aFb; В → аА}.

Определим правила для P(F): так как непосредственно выводимых нетерминалов не существует, то P(F) = 0.

Объединив полученные правила, можно записать грамматику Gэ, эквивалентную исходной:

S → aFb | aSb | аА; А → аА | aSb | aFb;

В → аА | aSb | aFb; F → bc | bFc.

Графическая модификация метода

Аналитическое преобразование по рассмотренному алгоритму оказывается довольно сложным. При автоматизированном преобразовании грамматик проще применить графическую модификацию этого метода. С этой целью каждому нетерминальному символу и каждой правой части правил из множества Р2 поставлена в соответствие вершина графа.

Из вершины с меткой U в вершину с меткой V направлено ребро, если в грамматике существует правило U → V.

В эквивалентную грамматику будут включены правила вида А → w, AÎVN; wÎ(VT È VN)* , если из вершины с меткой А существует путь в вершину с меткой w.

S → aFb | aSb | аА;

А → аА | aSb | aFb;

В → аА | aSb | aFb;

F → bc | bFc.

Получено то же множество правил Р, что и аналитическим методом.

Построение неукорачивающей грамматики

Грамматика, не содержащая правил с пустой правой частью, называется неукорачивающей грамматикой.

В грамматике с правилами вида А→ε длина выводимой цепочки при переходе от k-го шага к (k+1)-му уменьшается. Поэтому грамматики с правилами вида А→ε называются укорачивающими. Восходящий синтаксический разбор в укорачивающих грамматиках сложнее по сравнению с разбором в неукорачивающих грамматиках, т.к. при редукции необходимо отыскать такой фрагмент входной цепочки, в которую можно вставить пустой символ.

Покажем, что для произвольной КС-грамматики, порождающей язык без пустой цепочки, можно построить эквивалентную неукорачивающую КС-грамматику.

Построим множество всех нетерминальных символов грамматики G=(V_T, V_N, P, S), из которых выводится пустая цепочка, выделив следующие множества:

W1= {A | A→ε Î P},

Wn+1 = Wn È{B | B→ϕ Î P, ϕ Î W*_n }.

Затем найдем множество правил эквивалентной грамматики в два этапа:

а) удалив из множества P исходной грамматики правила с пустой правой частью P₁= P\{

A→ε | A→ε Î P};

б) получив новые правила A→ϕ' после удаления из каждого правила исходной грамматики A→ϕ Î P те нетерминалы, которые вошли в множество Wn по правилу:

P₁" = { A→ϕ' | A→ϕ Î P'; ϕ =ϕ₁Bϕ₂ | BÎW_n; ϕ'=ϕ₁Bϕ₂}.

Повторив п.б) для каждого нетерминала, принадлежащего множеству Wn, получим эквивалентную грамматику G = (V_T, V_N, P_э, S).

Пример. Пусть задана грамматика G со следующими правилами вывода: S → АbА | сАb | Bb; А → аАb | ε; В→АА|а. Необходимо:

1) построить множество нетерминалов, из которых выводится ε;

2) построить неукорачивающую грамматику, эквивалентную исходной.

Для того чтобы построить множество всех нетерминалов грамматики, из которых выводится пустая цепочка, выделим следующие множества:

W1 = {А | А → ε Î P};

W_m+1 = W_m È {В | В → ϕ Î Р, ϕ Î W*_m}.

Так как мы имеем правило А → ε Î Р, то можно построить множество W₁ = {A}, включающее нетерминал А.

Построим множество W₂. С нетерминалом А связан нетерминал В, т.е. существует правило В → АА и А Î W₁. Следовательно, W₂={A,B}.

W₃ = W₂, т. к. множество W₃={В|В → ϕ Î Р, ϕ Î W*_m } является пустым.

Исключив правило, содержащее пустую цепочку в правой части, получим неукорачивающую грамматику G1 следующего вида:

S → АbА | сАb | Bb | bA | Ab | cb | b;

A → aAb | ab;

В → АА | A | a.

2. Построение грамматики с продуктивными нетерминалами

Нетерминальный символ А называется непродуктивным (непроизводящим), если он не порождает ни одной терминальной цепочки, т.е. не существует вывода А →* х, где хÎV*_T. Поэтому представляет интерес удаление из грамматики всех непродуктивных нетерминальных символов. Рассмотрим, как для произвольной КС-грамматики можно построить эквивалентную КС-грамматику, все нетерминальные символы которой продуктивны. С этой целью выделяется множество W₁={A | A → ϕ Î P, ϕ Î V*_T}. Затем строится множество W₁, W₂, . . . , W_n+1 по следующим правилам:

W_n+1 = W_n È{B÷B → x Î P, x Î (VT È Wn)*}.

Пусть задана грамматика G со следующими правилами вывода: S → SA | BSb | bAb; A → aSa | bb; B → bBb | BaA. Построим множество продуктивных нетерминалов:

W₁ = {A}, т.к. в множестве P есть правило A → bb;

W₂ = {A, S}, т.к. имеется правило S → bAb и A Î W₁;

W₃ = W₂.

Все символы множества V_N\W_n являются непродуктивными, не используются в выводе никакой терминальной цепочки и их можно удалить из грамматики вместе со всеми правилами, в которые они входят. Грамматика G1, эквивалентная исходной грамматике, будет включать следующее множество правил:

S → SA | bAb; A → aSa | bb.

В грамматике G1 все нетерминалы продуктивны.

Построение грамматики, аксиома которой зависит от всех нетерминалов

Существует еще один тип нетерминальных символов, которые можно удалять из грамматики вместе с правилами, в которые они входят. Например, в грамматике G, заданной множеством правил P: S → aSb | ba; A → aAa | bba, нетерминал А не участвует ни в каком выводе, т.к. из аксиомы нельзя вывести цепочку, содержащую этот нетерминал. Поэтому из заданной грамматики можно удалить нетерминал А. Рассмотрим, как для произвольной КС-грамматики можно построить эквивалентную КС-грамматику, аксиома которой зависит от всех нетерминальных символов.

Для этого построим множество нетерминалов, от которых зависит аксиома. С этой целью выделим множества W₁, W₂, . . . , W_n+1 по следующим правилам:

W₁ = {S},

W_n+1 = W_n È{B | A → xBy Î P, A Î W_n}.

Нетерминал B ÎW_n тогда и только тогда, когда аксиома S зависит от B. Все нетерминалы, не содержащиеся в W_n, можно удалить из грамматики вместе с правилами, в которые они входят. Для этого построим множество нетерминалов, от которых зависит аксиома. С этой целью выделим множества W₁, W₂, . . . , W_n+1 по следующим правилам:

W₁ = {S},

W_n+1 = W_n È{B | A → xBy Î P, A Î W_n}.

Нетерминал BÎW_n тогда и только тогда, когда аксиома S зависит от B. Все нетерминалы, не содержащиеся в Wn, можно удалить из грамматики вместе с правилами, в которые они входят.

Пример. Пусть дана КС-грамматика G:

S → abS | ASa | ab; A → abAa | ab; B → bAab | bB.

Найдем нетерминалы, от которых зависит аксиома:

W₁ = {S},

W₂ = {S, A}, т.к. имеется правило S → Asa и S Î W₁;

W₃ = W₂.

Эквивалентная грамматика G₁, аксиома которой зависит от всех нетерминальных

символов:

S → abS | ASa | ab; A → abAa | ab.

Удаление правил с терминальной правой частью

Пусть в грамматике G имеется с терминальной правой частью A→β, где β Î V*_T. Тогда любой вывод с использованием этого правила имеет вид: S →* xAy → xβy. Здесь нетерминал А в сентенциальной форме xAy появился на предыдущем шаге вывода B → uAv.

Если в это правило вместо А подставить β, получим правило B → uβv. Тогда длина вывода некоторой цепочки сократится на один шаг. Следовательно, для того чтобы удалить терминальное правило грамматики A→β, необходимо учесть следующие правила:

а) если для нетерминала А больше нет правил, тогда во всех правых частях А заменяется на β;

б) если для нетерминала А есть другие правила, тогда добавляются новые правила, в которых А заменяется на β.

Пример. Пусть дана КС-грамматика G:

S → aSb | bAa | B; A → ABa | b | ε; B → ab | ba.

Удалим правила для нетерминала В. Тогда эквивалентная грамматика G1 будет включать следующие правила:

S → aSb | bAa | ab | ba; A → Aaba | Abaa| b | ε.

Построение эквивалентной праворекурсивной КС-грамматики

Некоторые специальные методы грамматического разбора неприменимы к леворекурсивным или праворекурсивным грамматикам, поэтому рассмотрим устранение левой или правой рекурсии. В общем случае избавиться от рекурсии в правилах грамматики невозможно, т.к. бесконечные языки порождаются грамматиками с конечным числом правил только благодаря рекурсии. Поэтому можно говорить лишь о преобразовании одного вида рекурсии в другой. Рассмотрим, как для любой леворекурсивной КС-грамматики построить эквивалентную праворекурсивную КС-грамматику.

Пусть нетерминал А - леворекурсивен, т.е. для него имеются правила следующего вида:

A → Ax₁ | Ax₂ | . . . | Ax_p | w₁| . . . | w_k, где x_i и w_j - цепочки над множеством V_T È V_N.

Введем дополнительные нетерминалы B и D и указанные правила заменим на эквивалентные им:

A → AB | D;

B → x₁ | x₂ | . . . | x_p;

D → w₁| w₂ | . . . | w_k.

В результате замены получим вывод, который имеет вид:

A → AB→ ABB → ABBB → . . . → AB* → DB*.

Таким образом, для нетерминала А можно определить эквивалентные правила:

A → DK;

K → BK | ε.

Выполняя подстановку D и B в эти правила, получим следующие праворекурсивные правила:

A → w1K| w2K | . . . | wkK;

K → x1K | x2K | . . . | xpK | ε.

Пример. Пусть задана грамматика G со следующими правилами вывода: S → Sa | ba. Требуется построить эквивалентную ей праворекурсивную грамматику.

Для решения задачи воспользуемся рассмотренным выше алгоритмом. В исходной грамматике один леворекурсивный нетерминал S. Построим для него вывод:

S → SB | D;

B → a; D → ba. Вывод из S имеет вид: S → SB→ SBB→ . . . →DB*.

Запишем эквивалентные правила для S: S → DK; K → BK | ε.

Подставим в эти правила B и D и получим эквивалентную праворекурсивную грамматику G₁:

S → baK; K → aK | ε.

Рассмотрим вывод цепочки baaaa в исходной леворекурсивной грамматике G:

S → Sa → Saa → Saaa → baaaa.

Эту же цепочку можно вывести в эквивалентной праворекурсивной грамматике G1:

S → baK → baaK → baaaK → baaaaK → baaaa.

Рекомендуемая литература

1 Кузовлев В.И.,Шкатов П.Н. Разработка САПР: в 10 кн. Кн.8: Математические методы анализа производительности и надежности САПР, М.: Высшая школа, 1990.

2 Глазунов Л.П. и др. Основы теории надежности автоматических систем упрвления. Учебное пособие для вузов. Л.: Энергоатомиздат, 1984 г.

Контрольные задания для СРС (тема 4) [1, 2, 7]

1. Классификация грамматик

2. Характерные особенности АСУ

Дата добавления: 2015-07-26; просмотров: 183; Нарушение авторских прав

Мы поможем в написании ваших работ!