
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Потери напора при установившемся равномерном движении жидкости (потери по длине)
Потери напора при равномерном движении пропорциональны длине участка русла, и поэтому их называют потерями напора по длине. Потери напора при резкоизменяющемся движении считаются сосредоточенными в месте, где поток деформируется, и их называют местными потерями напора µ.
Чтобы установить структуру зависимости для вычисления потерь напора по длине, рассмотрим потери напора hl на единицу длины, т.е. гидравлический уклон
Je =hl/l (2.1)
и определим, от каких характеристик потока он зависит. Будем рассматривать поток с расходом Q в круглоцилиндрической трубе диаметром D. Жидкость несжимаемая, ее механические свойства определяются плотностью r и динамическим коэффициентом вязкости µ .
Кроме того, так как напор представляет собой поток механической энергии, отнесенный к весовому расходу QB = rgQ, потери напора будут зависеть и от ускорения силы тяжести.
Все указанные параметры потока, кроме характеристик внутренней поверхности трубы, сравнительно легко измеряются. Для оценки влияния шероховатости стенок трубы на потери напора рассмотрим только такие поверхности, шероховатость которых описывается одной величиной — высотой выступов шероховатости  . Такую шероховатость называют зернистой(рис. 5.19,а). В действительности влияние на поток может оказыватьt не только высота выступов, но и их взаимное расположение на поверхности стенки, их очертание и т.п. Например, при прочих равных условиях выступы, имеющие очертание, представленное на рис. 5.19, б оказывают большее сопротивление течению жидкости и, следовательно, вызывают большие потери напора, чем выступы, представленные на рис. 5.19,в.
. Такую шероховатость называют зернистой(рис. 5.19,а). В действительности влияние на поток может оказыватьt не только высота выступов, но и их взаимное расположение на поверхности стенки, их очертание и т.п. Например, при прочих равных условиях выступы, имеющие очертание, представленное на рис. 5.19, б оказывают большее сопротивление течению жидкости и, следовательно, вызывают большие потери напора, чем выступы, представленные на рис. 5.19,в.

Стенка трубы
Рис. 5.19. Виды шероховатых стенок: а — зернистая шероховатость; бив — различные виды структурированной шероховатости; г — естественная шероховатость
При естественной шероховатости, имеющей место вследствие либо технологических особенностей изготовления труб (металлических, бетонных, деревянных и т.п.), либо вследствие их коррозии, либо по каким-то другим причинам (рис. 5.19,г), трудно бывает установить не только высоту выступов (хотя бы среднюю), но даже место, откуда надо отсчитывать эту высоту. О том, как ввести в гидравлические расчеты характеристику внутренней поверхности в случаях, представленных на рис. 5.19, будет сказано далее, а пока рассмотрим зернистую шероховатость, а геометрическую высоту выступов будем называть абсолютной шероховатостью Δ. Итак,
Je =f(r,µ ,Q, D , Δ , g). (2.2)
выберем в качестве независимых безразмерных произведений Re= rvD/µ, v2/gD.
Первое из них представляет собой известное число Рейнольдса ReD, а второе называют относительной шероховатостью Δr =Δ/D. Итак, используя анализ размерности,вместо (2.2) можно принять
Je=Je(ReD, Δr, v2/gD) (2.3)
где
ReD = uD/n, Δr = Δ/D.
Как показали экспериментальные исследования, числоРейнольдса можно использовать не только в качестве критерия для установления режима движения жидкости, но и как параметр, определяющий внутреннюю структуру турбулентного потока. Экспериментальное изучение потоков жидкости в трубах и каналах показало, что во многих практически важных случаях потери напора пропорциональны квадрату скорости и не зависят от вязкости жидкости. На этом основании, чтобы получить наиболее простую для практического использования структуру зависимости для Je, выражение (2.3) представляют в виде
Тогда, Je = (ReD,Δr)v2 / gD = 2f(ReD , Δr) *v2/2g *1/D (2.4)
Из этой зависимости получим выражение для потери напора hl, одновременно выделив скоростной напор v2/2g как величину, входящую в уравнение Бернулли в виде отдельного слагаемого. Обозначив 2f(ReD, 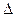 г) через Λ(ReD, Дг), получим формулу Вейсбаха—Дарси:
г) через Λ(ReD, Дг), получим формулу Вейсбаха—Дарси:
Hl = Λ(ReD , Δr)*lv2/D2g. (2.5)
Функция  (ReD,
(ReD, 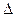 г) - Коэффициент гидравлического трения.
г) - Коэффициент гидравлического трения.
Вид функции  =
=  (ReD,
(ReD, 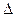 г) в виде графика был установлен экспериментальным путем и представлен И. Никурадзе, который выполнил в 1920-х годах свои исследования в Германии. Этот график, представленный на рис. 5.20, носит название графика Никурадзе.
г) в виде графика был установлен экспериментальным путем и представлен И. Никурадзе, который выполнил в 1920-х годах свои исследования в Германии. Этот график, представленный на рис. 5.20, носит название графика Никурадзе.

Рис. 5. 20 Схематизация графика Никурадзе для зависимости  =
=  (ReD,
(ReD, 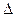 г)
г)
Он имеет следующие особенности. По горизонтальной оси отложено ReD в логарифмическом масштабе, чтобы охватить возможно больший диапазон значений ReD и в то же время достаточно детально представить область малых значений ReD < 104 относящихся к ламинарному движению. Для того, чтобы определить зависимость  от относительной шероховатости Δr , на этом же графике каждому фиксированному значению Δr ставится в соответствие отдельная кривая
от относительной шероховатости Δr , на этом же графике каждому фиксированному значению Δr ставится в соответствие отдельная кривая  =
=  ( ReD ).
( ReD ).
Вертикальные линии ReD = (ReD)'кр и ReD = (ReD)˝kp отделяют зону устойчивого ламинарного режима Л и зону, где может существовать только турбулентный режим Т, от переходной зоны П , где могут иметь место или тот илидругой режимы (см. разд. 5.13). При построении этого графика принимают (ReD)'кр = 2300, а (ReD)˝кр = 4000.
При ламинарном движении  не зависит от шероховатости и определяется по формуле
не зависит от шероховатости и определяется по формуле
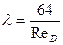 . (2.6)
. (2.6)
Подставив это выражение в (2.5), найдем
hl = Λ*lv2/D2g = 64/ReD*l/D*v2/2g = 64µ/vD*l/D*v2/2g = 32µ/g*l/D2=128/πg*µl/D4*Q
Q = πD2/4*V
Как видно из (5.113), потери напора при ламинарном движении пропорциональны средней скорости в первой степени или при заданном расходе Q обратно пропорциональны четвертой степени диаметра трубы. Этот результат экспериментально был установлен в 40-х годах прошлого века французским врачом Пуазейлем, и ламинарное движение жидкости в цилиндрических трубах называют течением Пуазейля. При числах ReD (см. рис. 5.20), лежащих в диапазоне (ReD)́̀̀кр < ReD< (ReD)˝кр , обычно предполагают, что движение турбулентное (ламинарное движение здесь неустойчиво, и, если не предпринять специальных мер (см. разд. 5.13), оно будет турбулентным). Поэтому на область П распространяют зависимости для  , экстраполируя их из области турбулентного режима движения Т.
, экстраполируя их из области турбулентного режима движения Т.
При турбулентном режиме движения выделяют три области: I, II и III (см. рис. 5.20), которые отделяются друг от друга штриховыми линиями нижних и верхних предельных чисел Рейнольдса: (ReD)́пред и (ReD)˝пред . Область I характеризуется тем, что в ней коэффициент гидравлического трения  не зависит от относительной шероховатости и все линии, отвечающие различным значениям
не зависит от относительной шероховатости и все линии, отвечающие различным значениям  , сливаются в одну, представляющую всю зону I. Эта линия, которая при ReD<105 на рис. 5.20 имеет вид прямой, достаточно хорошо аппроксимируется зависимостью, предложенной немецким ученым Блазиусом,
, сливаются в одну, представляющую всю зону I. Эта линия, которая при ReD<105 на рис. 5.20 имеет вид прямой, достаточно хорошо аппроксимируется зависимостью, предложенной немецким ученым Блазиусом,
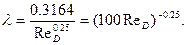 (2.8)
(2.8)
Подставив (2.8) в (2.5), получим, что в этой области hl ~ v1.75; область I называется областью гидравлически гладких труб; это следует понимать так: хотя шероховатость в трубах всегда имеется, но при ReD < (ReD)’пред она не оказывает влияния на потери напора. При больше значениях ReD в той же трубе коэффициент  будет зависеть от шероховатости
будет зависеть от шероховатости 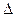 г.
г.
Область III характеризуется тем, что в ней коэффициент гидравлического трения  не зависит от числа Рейнольдса, а зависит только от относительной шероховатости
не зависит от числа Рейнольдса, а зависит только от относительной шероховатости 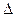 г; графически это проявляется в том, что линии
г; графически это проявляется в том, что линии  =
= 
 (ReD,
(ReD, 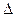 г) в этой области параллельны оси ReD. Поскольку здесь
г) в этой области параллельны оси ReD. Поскольку здесь  =
= 
 (
( 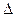 г) , то, согласно зависимости (2.7), потери напора hl~v2; поэтому область III называют областью квадратичного сопротивления.
г) , то, согласно зависимости (2.7), потери напора hl~v2; поэтому область III называют областью квадратичного сопротивления.
В области II коэффициент гидравлического трения зависит от ReD и от 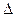 г; согласно (5.111), здесь h,~v1.75…2.0Учитывая, что переход из области П в область III обычно происходит при увеличении числа ReD, что достигается практически увеличением средней скорости в трубе, область II называют областью доквадратичного сопротивления.
г; согласно (5.111), здесь h,~v1.75…2.0Учитывая, что переход из области П в область III обычно происходит при увеличении числа ReD, что достигается практически увеличением средней скорости в трубе, область II называют областью доквадратичного сопротивления.
Никурадзе было сделано обобщение только для зернистой (искусственной) шероховатости; для естественной шероховатости график зависимости  =
= 
 (ReD,
(ReD, 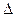 г) имеет в основном те же особенности, однако каждому виду естественной шероховатости следует поставить в соответствие высоту выступов некоторой фиктивной эквивалентной зернистой шероховатости, в зависимости от численного значения которой определяется величина
г) имеет в основном те же особенности, однако каждому виду естественной шероховатости следует поставить в соответствие высоту выступов некоторой фиктивной эквивалентной зернистой шероховатости, в зависимости от численного значения которой определяется величина  . Эквивалентность некоторой зернистой шероховатости и заданной естественной шероховатости устанавливается на основе гидравлических исследований потерь напора в трубах с обеими указанными (зернистой и естественной) шероховатостями; значение l в обеих трубах должно быть одинаковым в области квадратичного сопротивления.
. Эквивалентность некоторой зернистой шероховатости и заданной естественной шероховатости устанавливается на основе гидравлических исследований потерь напора в трубах с обеими указанными (зернистой и естественной) шероховатостями; значение l в обеих трубах должно быть одинаковым в области квадратичного сопротивления.
При естественной шероховатости расчетная высота выступов эквивалентной зернистой шероховатости назначается с помощью специальных таблиц, где значение Δ определяется в зависимости от словесного описания состояния внутренней поверхности трубы, которое зависит от технологии изготовления и монтажа трубы, от условий ее эксплуатации и т.п. (табл. 5.1).
В газопроводах потери энергии часто оцениваются не как потери напора hl, а как потери давления 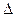 р по длине. При этом формула Вейсбаха—Дарси представляется в виде
р по длине. При этом формула Вейсбаха—Дарси представляется в виде
 . (2.9)
. (2.9)
а коэффициент гидравлического трения рассчитывается так же, как для несжимаемых жидкостей.
Таблица 5.1. Значения параметров шероховатости для разных материалов
| Поверхность | Высота выступов 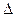 , мм , мм
| Коэффициент шероховатости.  n n
|
| Исключительно гладкие поверхности | ||
| (эмалированные, глазурованные и т.п.) | 0,02 | 0,010(0,009—0,013) |
| Цементная штукатурка: | ||
| ожелезненная или чисто заглаженная | 0,1(0,02...0,3) | <0,010 |
| обычная | 0,3(0,1...0,8) | <0,012 |
| Трубы стальные | ||
| бесшовные новые чистые | 0,014(0,01...0,02) | 0,010(0,009-0,011) |
| сварные новые чистые | 0,05(0,03...0,12) | 0,012(0,011—0,013) |
| умеренно заржавленные | 0,5(0,3...0,7) | 0,014(0,013-0,015) |
| Трубы чугунные: | ||
| новые | 0,7(0,25... 1,0) | 0,015(0,013-0,016) |
| корродированные | 1,3(1,00...1,5) | 0,020(0,016-0,025) |
| Деревянные лотки из досок: | ||
| строганых | 2(0,5...8,0) | 0,014(0,010-0,018) |
| нестроганых | 3(0,8—10,0) | 0,016(0,0012-0,019) |
| Бетонированная стенка | 2(0,3...5,0) | 0,013(0,012-0,015) |
| Кирпичная кладка | 3(1,0...6,0) | 0,015(0,013-0,017) |
| Бутовая кладка | 20(5...70) | 0,021 (0,017-0,025) |
| Булыжная мостовая | 25(15...3О) | 0,022(0,020.-0,025) |
| Канализационные трубы: | ||
| бетонные и железобетонные | 0,014 | |
| керамические | 1,25 | 0,013 |
| Земляные каналы прямолинейные: | ||
| чистые, после эксплуатации | 50(15.200) | 0,022(0,018-0,024) |
| с короткой травой и водорослями | 0,028(0,024...0,033) | |
| чистое дно, кустарник на откосах | 0,06(0,04-0,08) | |
| Естественные водотоки (реки): | ||
| чистые прямолинейные без перекатов и | ||
| омутов | 0,030(0,025.-0,033) | |
| чистые извилистые с омутами и | ||
| перекатами | 0,040(0,033-0,045) | |
| очень заросшие с застрявшими | ||
| тяжелыми стволами и порослью | 0,11(0,075-0,15) |
Приводятся наиболее вероятные значения для средних условий; в скобках указываются возможные пределы колебаний.
графику является табл. 5.1, в которой представлены значения D для различных трубопроводов в зависимости от их материала, технологии изготовления и монтажа, условий эксплуатации. График рис. 5. 21 называют графиком Кольбрука—Уайта, а в США — графиком Муди.
Зависимости  =
=  (ReD,
(ReD, 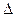 г) для турбулентного режима движения хорошо аппроксимируются формулой Альтшуля (при
г) для турбулентного режима движения хорошо аппроксимируются формулой Альтшуля (при 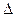 г < 0,007):
г < 0,007):
 0,25 (2.10)
0,25 (2.10)
Коэффициент гидравлического трения 'к
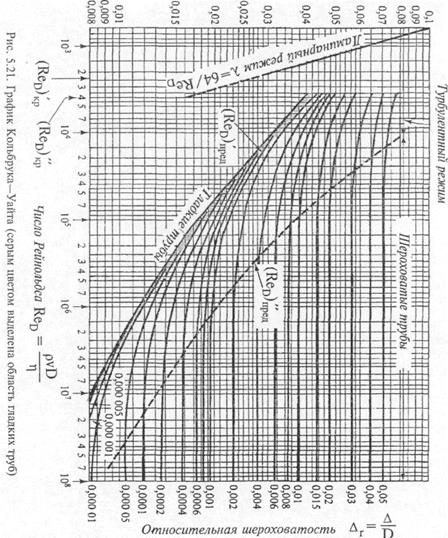
а в области квадратичного сопротивления формулой Шифринсона:
 (2.11)
(2.11)
В области гладкого сопротивления ( 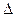 г~ 0) формула (2.10) дает хорошее совпадение с зависимостью Блазиуса (2.8).
г~ 0) формула (2.10) дает хорошее совпадение с зависимостью Блазиуса (2.8).
| <== предыдущая страница | | | следующая страница ==> |
| Журнал наблюдений | | | Формула Шези |
Дата добавления: 2015-07-26; просмотров: 478; Нарушение авторских прав

Мы поможем в написании ваших работ!