Т Е К С Т Л Е К Ц И И

Вероятностный смысл математического ожидания состоит в том, что оно приближенно равно (в особенности для большого числа испытаний) среднему арифметическому значению случайной величины.

Пример. Случайная дискретная величина 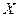задана следующим законом распределения:

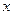
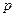
	0,3	0,4	0,3

Определить математическое ожидание случайной дискретной величины .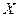

Решение.

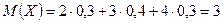
Ответ.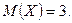

Свойства математического ожидания.

1. Математическое ожидание постоянной величины равно самой постоянной:

.

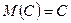1. Постоянный множитель можно выносить за знак математического ожидания, т.е.

.

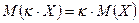1. Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е.

.

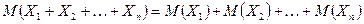1. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий, т.е.

.

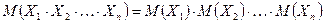1. Если все значения случайной величины увеличить (уменьшить) на постоянную С, то на эту же постоянную С увеличится (уменьшится) математическое ожидание этой случайной величины:

.

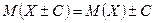1. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:

.

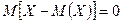Отклонение (рассеяние, разброс) случайной величины относительно среднего значения характеризуют дисперсия и среднее квадратичное отклонение. Слово дисперсия означает «рассеяние».

Определение. Дисперсией дискретной случайной величины 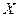называется математическое ожидание квадрата разности случайной величины 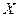и ее математического ожидания:

.

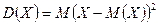Формула дисперсии в развернутом виде:

.

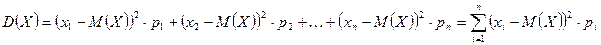При вычислении дисперсии удобно пользоваться следующей формулой:

.

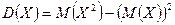Пример. Случайная дискретная величина 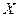задана следующим законом распределения:

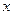
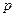
	0,3	0,4	0,3

Определить дисперсию случайной дискретной величины .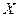

Решение.

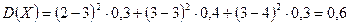
Ответ.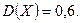

Свойства дисперсии.

1. Дисперсия постоянной величины С равна нулю:

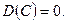
1. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

.

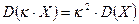1. Дисперсия суммы независимых случайных величин равна сумме их дисперсий:

.

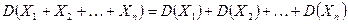1. Если все значения случайной величины увеличить на постоянную С, то значение дисперсии этой случайной величины не изменится:

.

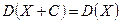Дисперсия имеет размерность квадрата случайной величины. Иногда, для характеристики рассеивания, удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Такая величина – среднеквадратичное отклонение.

Определение. Среднеквадратичным отклонением дискретной случайной величины называется корень квадратный из ее дисперсии:

.

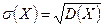1. Числовые характеристики непрерывной случайной величины.

Определение. Математическим ожиданием непрерывной случайной величины 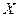с плотностью распределения 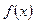называется выражение

.

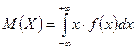Если непрерывная случайная величина 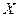может принимать значения только на конечном отрезке 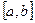, то .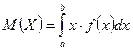

Определение. Дисперсией непрерывной случайной величины 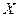называется значение интеграла

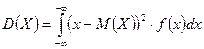
или

.

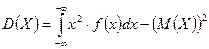Определение. Среднеквадратичным отклонением непрерывной случайной величины 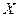называется корень квадратный из дисперсии

.

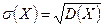по дисциплине «Стратегический менеджмент»

на тему:

Стратегическое управление: концептуальные основы и необходимость использования на современном этапе

Севастополь – 2012

Дата добавления: 2014-03-08; просмотров: 297; Нарушение авторских прав

Мы поможем в написании ваших работ!