Постановка задачи ЦЛП

Целочисленное программирование ориентировано на решение задач математического программирования, в которых все или некоторые переменные должны принимать только целочисленные значения.

Задача называется полностью целочисленной, если условие целочисленности наложено на все ее переменные; когда это условие относится лишь к некоторым переменным, задача называется частично целочисленной. Если при этом целевая функция и функции, входящие в ограничения, линейные, то задача является линейной целочисленной.

Несмотря на то, что к настоящему времени разработан ряд методов решения целочисленных задач, ни один из них не обеспечивает желаемой эффективности соответствующих вычислительных процедур, что особенно проявляется при увеличении размерности задачи. Таким образом, в отличие от задач линейного программирования, время решения которых относительно невелико, реализация целочисленных алгоритмов в ряде случаев весьма затруднительна.

Одна из основных трудностей в целочисленном программировании связана с эффектом ошибки округления, возникающим при использовании цифровых ЭВМ. Даже наличие алгоритмов, применимых для решения задач с целочисленными коэффициентами и позволяющих обойтись без оперирования дробями (и, следовательно, избежать влияния ошибок округления), не упрощает ситуации, поскольку такие алгоритмы (в ряде случаев) сходятся чрезвычайно медленно.

Методы решения задач целочисленного программирования можно классифицировать как (1) методы отсечений и (2) комбинаторные методы.

Исходной задачей для демонстрации возможностей методов отсечений, используемых при решении линейных целочисленных задач, является задача с ослабленными ограничениями, которая возникает в результате исключения требования целочисленности переменных. По мере введения специальных дополнительных ограничений, учитывающих требование целочисленности, многогранник допустимых решений ослабленной задачи постепенно деформируется/до тех пор, пока координаты оптимального решения не станут целочисленными. Название «методы отсечений» связано с тем обстоятельством, что вводимые дополнительные ограничения отсекают (исключают) некоторые области многогранника допустимых решений, в которых отсутствуют точки с целочисленными координатами.

В основе комбинаторных методов лежит идея перебора всех до­пустимых целочисленных решений. Разумеется, на первый план здесь выдвигается проблема разработки тестовых процедур, позволяющих непосредственно рассматривать лишь (относительно небольшую) часть указанных решений, а остальные допустимые решения учитывать некоторым косвенным образом.

Задача целочисленного программирования (ЦЛП) формулируется так же, как и задача ЛП, но включается дополнительное требование, состоящее в том, что значения переменных, составляющих оптимальное решение должны быть целыми неотрицательными числами:

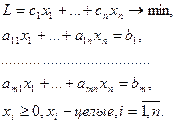(1)

Симплекс – метод не гарантирует целочисленности решения задачи (1), поэтому для отыскания оптимального целочисленного решения задачи ЦЛП требуются специальные методы.

Один из таких методов – метод отсечения, приводящий к целочисленному решению за конечное число шагов, предложен американским математиков Р. Гомори. Идея метода следующая.

С помощью симплекс – метода решается задача ЛП без условия целочисленности. Если оптимальное решение получается нецелочисленным, то вводится дополнительное ограничение, которое, уменьшая многогранник допустимых решений (отсекая некоторую его часть), не исключает из него целочисленных точек. Если оптимальное решение задачи ЛП с дополнительным ограничением целочисленное, то вычисления заканчивают; если же оптимальное решение содержит хотя бы одну дробную компоненту, добавляют новое дополнительное ограничение.

Процесс присоединения дополнительных ограничений повторяют до тех пор, пока либо не будет найдено целочисленное оптимальное решение, либо показано, что задача не имеет целочисленных решений.

После добавления дополнительного ограничения в задачу ее удобно решать с помощью двойственного симплекс-метода.

Дата добавления: 2015-07-26; просмотров: 229; Нарушение авторских прав

Мы поможем в написании ваших работ!