
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Методы нахождения множества Парето
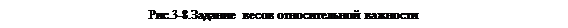
Определим формально условие эффективности решения по Парето.
Пусть имеем множество альтернатив X, для каждого элемента xÎX которого определен вектор критериев  .
.
Пусть критерии ui(х) и альтернативы x,yÎX обладают следующим свойством:
ui(х)³ ui(y), i=1,…,n; u(x) ≠ u(y) Þ x f y,
т.е. решение x предпочтительнее решения y всякий раз, когда значения всех критериев для альтернативы x не меньше, чем для y. В этом случае говорят, что решение x доминирует над решением y.
Если для некоторого решения xÎX не существует решения yÎX, такого что 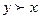 , то решение x называется эффективным на множестве X, а множество всех эффективных решений – множеством Парето или эффективной границей множества X.
, то решение x называется эффективным на множестве X, а множество всех эффективных решений – множеством Парето или эффективной границей множества X.
Из данного определения следует, что если решение x не является эффективным, то для него в множестве Парето найдется решение y, доминирующее над x. Поэтому лучшее среди решений из X будет принадлежать множеству Парето при любых (разумных) предпочтениях ЛПР. Это в свою очередь позволяет при решении оптимизационных задач исследовать не все множество X, а лишь его эффективную границу.
Нахождение множества Парето – самостоятельная, иногда довольно сложная задача, для решения которой имеются многочисленные методы. Простейший из них основан на следующем результате [20].
Теорема 2.1. Пусть множество векторных оценок U решений из X строго выпукло, ограничено и замкнуто. Для того чтобы решение x*ÎX было эффективным, необходимо и достаточно, чтобы существовали такие неотрицательные коэффициенты 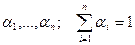 , для которых
, для которых 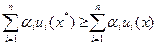 для любого другого решения xÎX.
для любого другого решения xÎX.
Множество векторных оценок U строится путем отображения множества сравниваемых альтернатив X из пространства альтернатив X* в пространство критериев 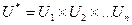 , где Ui ( i = 1,…,n ) – множество возможных для альтернатив из X значений i-го критерия. Ограниченность и замкнутость множества U гарантирует существование эффективных решений, а условие
, где Ui ( i = 1,…,n ) – множество возможных для альтернатив из X значений i-го критерия. Ограниченность и замкнутость множества U гарантирует существование эффективных решений, а условие 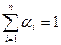 необходимо для того, чтобы исключить из рассмотрения тривиальный случай
необходимо для того, чтобы исключить из рассмотрения тривиальный случай 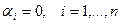 .
.
 |
На рис. 3-9 показаны пространство U* и строго выпуклое множество U ( т.е. такое множество, которое содержит отрезок, соединяющий любые две точки этого множества, внутри себя) и прямая А, заданная уравнением
 , где К – константа.
, где К – константа.
По мере увеличения значения К прямая будет перемещаться вверх параллельно самой себе, пока не превратится в касательную A* к границе множества U в точке u*. Соответствующее этой точке решение x* согласно теореме будет эффективным.
Изменяя значения коэффициентов α1 и α2 легко найти и другие эффективные точки. В результате будет найдено множество Парето, выделенное на рис. 3-9 жирной линией. Граничные точки множества Парето определяются перемещением прямых, для которых α1=0, α2=1 (точка B) и α1=1, α2=0 (точка С).
Рассмотрим теперь случай, когда множество U не является выпуклым (рис.3-10). Тогда для точки u*, лежащей на границе множества U, нельзя подобрать коэффициенты α1 и α2, при которых выполняется условие теоремы 2.1. Тем не менее северо-восточный угол Y(u*) с вершиной в точке u* не содержит точек из U (кроме точки u*) и, следовательно, решение u* является эффективным. Условие, позволяющее находить эффективные решения для невыпуклых множеств U, получено Гермейером [7].
Теорема 2.2. Пусть множество Парето ограничено и замкнуто, a ui(x) > 0 для всех i=1,…,n для всех xÎX. Для того чтобы решение x* было эффективным, необходимо и достаточно, чтобы существовали строго положительные коэффициенты
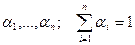 , удовлетворяющие условию
, удовлетворяющие условию
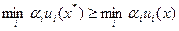 , для всех xÎX, причем равенство имеет место тогда и только тогда, когда ui(x*) = ui(x) для всех i=1,..,n.
, для всех xÎX, причем равенство имеет место тогда и только тогда, когда ui(x*) = ui(x) для всех i=1,..,n.
Приведенный результат особенно полезен в ситуациях, когда требуется установить, является ли данное решение эффективным или оно может быть улучшено хотя бы по одному критерию.
Пример 3-9. Пусть X представлено двумерной областью, удовлетворяющей неравенствам

а каждое решение xÎX оценивается по критериям 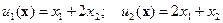 .
.
В X выберем решение x*=(0,2; 0,5). Если x* является эффективным решением, то из теоремы 2.2 имеем
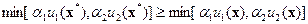 для всех xÎX.
для всех xÎX.
Неизвестные коэффициенты α1 и α2 можно определить, решив систему уравнений
 .
.
Поскольку u1(x*)=1,2, u2(x*)=0,9, то из системы имеем α1 = 0,43, α2=0,57. Уравнение

задает прямую A (рис.3-11), проходящую через начало координат и точку x* . Если x* лежит на границе множества X, то наше предположение верно и x* – эффективное решение. В противном случае эффективное решение 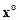 , доминирующее над x*, найдем, двигаясь по прямой А до пересечения с границей множества X.
, доминирующее над x*, найдем, двигаясь по прямой А до пересечения с границей множества X.
Чтобы найти 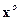 достаточно определить
достаточно определить

при условии выполнения ограничений

 .
.
В общем случае для этого требуется решить соответствующую задачу линейного программирования. В данном примере  = (0,3; 0,7) легко определить непосредственно из рис. 3-11.
= (0,3; 0,7) легко определить непосредственно из рис. 3-11.
Сложность задачи отыскания множества Парето резко возрастает, если X не удовлетворяет условиям выпуклости и замкнутости, имеет изолированные точки, состоит из отдельных несвязных частей или оценивается по критериям, не являющимся гладкими функциями. В этих случаях более перспективными могут оказаться приближенные методы нахождения множества Парето.
Следуя [10] опишем один из простейших алгоритмов приближенного на хождения множества Парето. Алгоритм содержит следующие шаги.
1. В пространстве критериев 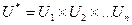 с помощью случайной последовательности генерируются пробные точки
с помощью случайной последовательности генерируются пробные точки  . Если соответствующее вектору u(x) решение x принадлежит множеству X, то u(x)ÎU. Множество таких точек обозначим через D.
. Если соответствующее вектору u(x) решение x принадлежит множеству X, то u(x)ÎU. Множество таких точек обозначим через D.
2. Выбирается произвольный вектор ui и сравнивается со всеми остальными векторами из D. Все векторы uj такие, что ui 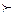 uj, исключаются из множества D.
uj, исключаются из множества D.
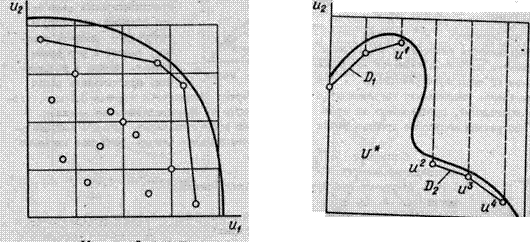
3. Шаг 2 повторяется до тех пор, пока в D не окажутся только векторы, не доминирующие друг над другом. Соединив оставшиеся в D точки (рис.3-12), получим ломаную, являющуюся приближением к множеству Парето, показанному жирной линией.
С увеличением числа точек, генерируемых в D на шаге 1, ломаная, построенная на шаге 3, будет приближаться к точной эффективной границе.
Рассмотренный алгоритм легко реализуется, а быстродействие современных ЭВМ позволяет генерировать достаточное число пробных точек в множестве D, обеспечивая тем самым требуемую точность нахождения множества Парето. При этом ни на множество X, ни на используемые критерии по сути не накладываются какие-либо ограничения.
Очевидным недостатком данного алгоритма является необходимость генерировать пробные точки во всем пространстве U*. Это представляется излишним и существенно увеличивает трудоемкость шага 2. Чтобы сократить объем вычислений, производимых на этом шаге, модифицируем процедуру построения множества пробных точек следующим образом.
1. С помощью случайной последовательности в (n-1)-мерном пространстве  генерируется точка
генерируется точка  , не содержащая n-й компоненты.
, не содержащая n-й компоненты.
2. Значение n-го критерия un(x) полагается равным  и формируется начальная пробная точка
и формируется начальная пробная точка  .
.
3. Если точке u(х) соответствует решение xÎX, то она включается в множество D. В противном случае значение n-го критерия в u(x) уменьшается с некоторым шагом h до тех пор, пока условие xÎX не окажется выполненным. Полученная таким образом пробная точка 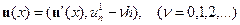 включается в множество D.
включается в множество D.
При таком способе построения множества D пробные точки как бы опускаются вдоль n-ой координаты пространства критериев U* на границу множества U(рис.3-13).
Поэтому в множество D включаются только точки, приближенно описывающие эту границу. Из 6 точек, составляющих согласно рис.3-13 множество  в множество Парето войдут только U1,U2,U3,U4.
в множество Парето войдут только U1,U2,U3,U4.
Путем попарного сравнения соответствующих этим точкам решений ЛПР должно выбрать решение, лучшее с его точки зрения.
 |
 |
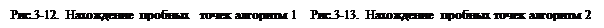
3.4.Подход исследования операций
Модели, связанные с принятием решений, активно используются в исследовании операций. Исследование операций — сложившаяся научная дисциплина, хорошо известная в современном мире. Как определяет Е.С. Вентцель [1], под исследованием операций понимают применение математических, количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности.
Основными этапами решения любой задачи в исследовании операций являются:
1) построение модели;
2) выбор критерия оптимальности;
3) нахождение оптимального решения.
Для подхода исследования операций характерны следующие особенности.
1. Используемые модели носят объективный характер. Построение моделей рассматривается в рамках исследования операций как средство отражения объективно существующей реальности. Когда модель, правильно отражающая действительность, найдена, критерий оптимальности установлен, оптимальное решение может быть получено единственно возможным образом. «Другими словами, опираясь на одни и те же данные, различные специалисты-аналитики должны получать одинаковые результаты» [2]. Это требование, предложенное Г. Вагнером, весьма примечательно. Оно определяет, что деятельность людей, описываемая моделью, подчинена требованиям целесообразности.
2. Существует объективный критерий успехов в применении методов исследования операций. Если проблема, требующая решения, ясна и критерий определен, то аналитический метод сразу показывает, насколько новое решение лучше старого. Оптимальное решение проблемы бессмысленно оспаривать.
Опишем две классические задачи исследования операций.
Первая из них получила название обобщенной транспортной задачи [2]. Пусть имеется большая авиакомпания, перевозящая пассажиров по различным маршрутам. Руководство компании определяет, какие самолеты (по вместительности) и сколько самолетов должны обслуживать различные маршруты. Считается, что известны потоки пассажиров между разными городами и общее число имеющихся самолетов различного типа. Требуется распределить самолеты по маршрутам так, чтобы минимизировать расходы на их обслуживание.
Вторая задача получила название задачи о назначениях. Предполагается, что необходимо распределить заданное число работ среди исполнителей так, чтобы каждый исполнитель выполнял одну работу. Стоимость выполнения каждой из работ каждым исполнителем известна. Нужно распределить работы так, чтобы суммарная стоимость их выполнения была минимальной.
Словесному описанию этих двух задач соответствует четкое математическое описание [2], представляющее собой математическую модель.
| <== предыдущая страница | | | следующая страница ==> |
| Парето оптимальные решения | | | Обсуждение многокритериальности |
Дата добавления: 2015-07-26; просмотров: 681; Нарушение авторских прав

Мы поможем в написании ваших работ!