Система линейных алгебраических уравнений. Основная и расширенная матрица. Совместная, несовместная и однородная системы уравнений

Система линейных алгебраических уравнений, содержащая 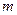уравнений и 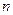неизвестных имеет следующий вид:

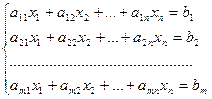(1)

Обозначим матрицу-столбец из неизвестных через X и матрицу-столбец из свободных членов через B.

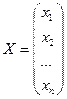– столбец неизвестных, 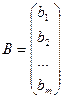– столбец свободных членов.

Тогда систему (1) можно записать в виде: 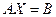, (2)

где 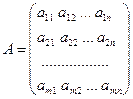– основная матрица системы.

Уравнение (2) называется матричным уравнением. Перепишем уравнение (2) следующим образом .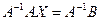

Тогда получим решение матричного уравнения в виде: 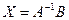(3)

Матрицу 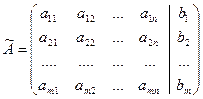называют расширенной матрицей системы.

Определение.Система линейных алгебраических уравнений называется прямоугольной, если 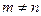, и квадратной, если .

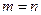Определение.Система линейных алгебраических уравнений называется однородной, если 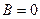, т.е., если столбец свободных членов состоит из одних нулей.

Определение. Система линейных алгебраических уравнений называется неоднородной, если .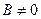

Определение. Система линейных алгебраических уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Определение. Совместная система линейных алгебраических уравнений называется определенной, если она имеет только одно решение, и неопределенной, если она имеет более одного решения.

Определение.Две системы называются эквивалентными, если любое решение одной из них является решением и другой системы. Заметим, что все несовместные системы являются эквивалентными.

Элементарные преобразования системы линейных уравнений:

1. перестановка любых двух уравнений;

2. умножение обеих частей одного уравнения на любое число отличное от нуля;

3. прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число.

Элементарные преобразования переводят данную систему в эквивалентную.

Дата добавления: 2015-07-26; просмотров: 290; Нарушение авторских прав

Мы поможем в написании ваших работ!