Репрограммируемые ПЗУ

Отличаются от вышеперечисленных возможностью многократной записи и стирания информации. К таким ПЗУ относятся и современные флеш-карты.

3.11 Аналого – цифровое и цифро – аналоговое преобразование

Назначение, основные свойства и классификация.

В электронных системах одинаково широко используется обработка информации, представленной в аналоговой и цифровой формах. Объясняется это тем, что первичная, исходная информация о различных физических величинах и процессах носит, как правило, аналоговый характер. Обработку же этой информации удобнее вести в цифровой форме. Использование полученных после цифровой обработки результатов также в большинстве случаев требует их аналогового представления. Следовательно, любая система, использующая цифровые методы обработки информации, должна содержать устройства взаимного преобразования аналоговых и цифровых сигналов. Роль таких устройств выполняют аналого-цифровые и цифро-аналоговые преобразователи (АЦП и ЦАП).

Аналого-цифровой преобразователь - устройство, предназначенное для преобразования непрерывно изменяющейся во времени аналоговой физической величины в эквивалентные ей значения числовых кодов.

Цифро-аналоговый преобразователь - устройство, предназназченное для преобразования входной величины, представленной последовательностью числовых кодов, в эквивалентные им значения заданной физической величины.

В качестве аналоговой физической величины, оговоренной в данных определениях, в общем случае могут фигурировать различные параметры, например угол поворота, линейное перемещение, давление жидкости или газа и т. д. В дальнейшем под этой величиной будем понимать напряжение либо ток, которые, при необходимости, можно легко преобразовать в другие физические величины.

Основным вопросом, с которым приходится сталкиваться при проектировании и использовании ЦАП и АЦП, является вопрос адекватности полученного в результате преобразования сигнала исходному физическому процессу, т. е. вопрос точности преобразования. Поэтому рассмотрим алгоритмы этих преобразований с точки зрения погрешностей, возникающих при их выполнении.

Процесс аналого-цифрового преобразования предполагает последовательное выполнение следующих операций:

1. выборка значений исходной аналоговой величины в некоторые наперед заданные дискретные моменты времени, т. е. дискретизация сигнала по времени;

2. квантование (округление до некоторых известных величин) полученной в дискретные моменты времени последовательности значений исходной аналоговой величины по уровню;

3. кодирование - замена найденных квантованных значений некоторыми числовыми кодами.

Проиллюстрируем эту последовательность действий с помощью рисунка.

Пусть задана некоторая аналоговая зависимость u(t). Для получения ее дискретного эквивалента U(nT_д)={U(0),U(Tд),U(2Tд),…} необходимо провести выборку ее значений в дискретные моменты времени nTд, где n=0,1,2... целое число. Постоянная величина Tд - носит название периода выборки или периода дискретизации, а сам процесс замены исходной аналоговой функции u(t) некоторой дискретной функцией U(nT_д) называется дискретизацией сигнала во времени. Следует отметить, что полученная дискретная функция U(nT_д) относительно самого сигнала u(t) носит по-прежнему аналоговый характер, так как может принимать бесконечное число различных значений.

Операция квантования по уровню дискретной функции U(nT_д) заключается в отображении бесконечного множества ее значений на некоторое конечное множество значений U*_n, называемых уровнями квантования. Для выполнения этой операции весь динамический диапазон D= U(nT_д)_max - U(nT_д)_min изменения дискретной функции U(nT_д) разбивают на некоторое заданное число уровней N и производят округление каждой величины U(nT_д) до ближайшего уровня U*_n. Величина h=D/N носит название шага квантования. Результатом операции квантования по уровню является дискретная функция U*_n, которая может принимать N+1 значение.

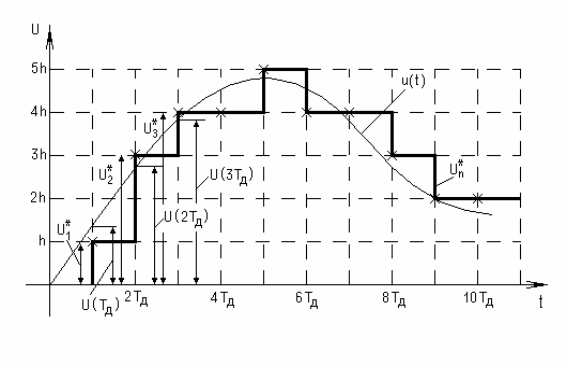
Для выполнения последней операции необходимо выбрать некоторый код К={К₁, К₂...}, способный отображать не менее (N+1)-го значения, и каждому дискретному значению U*_n поставить в соответствие некоторый код К_i В простейшем случае в качестве кода может быть использована последовательность чисел, соответствующих порядковым номерам уровней квантования. При таком выборе кода представленная на рис... функция u(t) может быть заменена последовательностью десятичных чисел: K_n={0, 1, 3, 4, 4, 5, 4, 4, 3, 2, 2), или в двоичной форме K_n ={000, 001, 011, 100, 100, 101, 100, 100, 011, 010, 010}.

Как следует из описанного алгоритма, переходы от исходной функции u(t) к дискретной U(nT_д) и далее к квантованной по уровню U*_n сопряжены с некоторой потерей информации. На этапе же кодирования подобные потери отсутствуют. Рассмотрим вопрос потери информации более подробно.

Предположим, что исходная аналоговая функция u(t) может быть представлена в виде конечной суммы гармонических сигналов, т. е. ее частотный спектр ограничен:

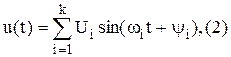
Тогда согласно известной из теории информации теореме Котельникова, если период дискретизации T_д отвечает условию

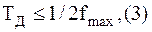
где f_max - частота максимальной гармоники исходного сигнала u(t), дискретные значения U(nT_д) полностью определяют исходную зависимость u(t), и замена аналоговой функции u(t) на дискретную U(nT_д) не сопряжена с искажением вида исходной зависимости, так как по U(nT_д) можно однозначно восстановить исходный вид u(t). Следовательно, при выполнении условия (....) погрешность преобразования на этапе дискретизации по времени отсутствует.

Процесс квантования по уровню дискретной функции U(nT_д) всегда связан с внесением некоторой погрешности 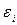, значение которой (см. рис... ) определяется неравенством .

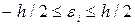Величина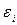,носит название шума квантования и однозначно определяется числом допустимых значений функции U*_n, т. е. разрядностью используемого числового кода.

Поэтому погрешность аналого-цифрового преобразования, обусловленная шумом квантования, при увеличении разрядности выходного кода может быть уменьшена до сколь угодно малой величины. Но в отличие от погрешности дискретизации по времени она принципиально присуща данному алгоритму и не может быть сведена к нулю выбором параметров устройства.

Рассмотренные погрешности обусловлены самим алгоритмом аналого-цифрового преобразования. Кроме них в реальных АЦП возникают погрешности, связанные с неидеальностью используемой элементной базы, т. е. инструментальные погрешности.

Процесс цифро-аналогового преобразования предполагает последовательное выполнение следующих операций: формирование в заданном диапазоне изменения выходного сигнала М его дискретных значений U*_M, отличающихся на некоторое значение 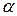, и постановка каждому сформированному уровню в соответствие некоторого кода K_i; последовательное, с заданным временным интервалом Т₁, присвоение выходному сигналу значений выделенных уровней, соответствующих входной последовательности кодов К_i.

Если предположить, что 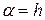и T₁=T_д, то результатом цифро-аналогового преобразования полученной ранее последовательности кодов K_n будет, показанная на рис..., ступенчатая функция U*_n. Эта функция, хотя и непрерывна во времени, но остается дискретной по уровню, что является результатом погрешности, обусленной шумом квантования. Сам процесс цифро-аналогового образования не вносит собственных принципиальных погрешностей, а лишь материализует погрешности, полученные в АЦП. Реально возникающие при преобразовании погрешности носят чисто инструментальный характер.

Подводя итог сказанному, отметим, что погрешности, обусленные самим алгоритмом работы, возникают только на этапе аналого-цифрового преобразования и их уменьшение требует уменьшения периода дискретизации T_д и шага квантования h.

Дата добавления: 2014-03-11; просмотров: 374; Нарушение авторских прав

Мы поможем в написании ваших работ!