
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Второй замечательный предел
Пример 5.1. Найти 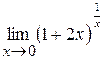 .
.
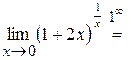
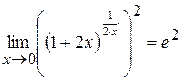 , так как
, так как 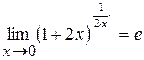 .
.
Пример 5.2. Найти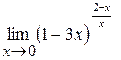 .
.
Воспользуемся следствием из второго замечательного предела.
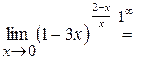
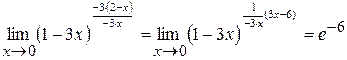 ,
,
так как 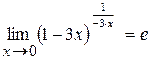 .
.
Пример 5.3. Вычислить 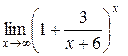 .
.
Имеет место неопределённость 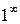 , воспользуемся вторым замечательным пределом
, воспользуемся вторым замечательным пределом 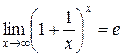 . Умножим и разделим показатель степени на
. Умножим и разделим показатель степени на 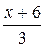 .
.
В результате получим 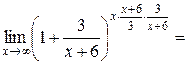
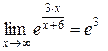 , так как
, так как 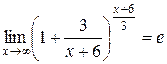 , а
, а 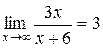 (см. п. 1).
(см. п. 1).
Пример 5.4. Вычислить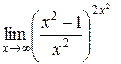 .
.
Для раскрытия неопределённости 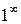 необходимо воспользоваться формулой
необходимо воспользоваться формулой 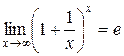 . Разделим почленно числитель на знаменатель.
. Разделим почленно числитель на знаменатель.
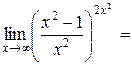
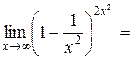
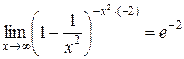 , так как
, так как 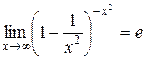 .
.
Пример 5.5. Найти 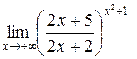 .
.
Имеет место неопределённость 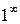 . Предварительно представим дробь
. Предварительно представим дробь 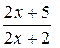 в виде суммы числа 1 и б.м. функции при
в виде суммы числа 1 и б.м. функции при  . Это можно сделать несколькими способами. Например,
. Это можно сделать несколькими способами. Например,
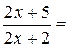
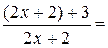
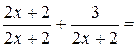
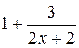 или
или
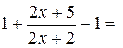
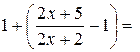
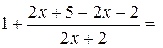
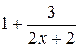 .
.
Таким образом, 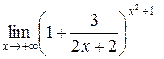 . Умножим и разделим показатель степени на дробь
. Умножим и разделим показатель степени на дробь 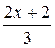 . Получим,
. Получим,
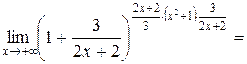
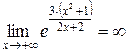 , так как
, так как
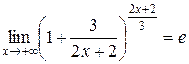 и
и 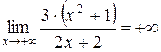 (поскольку степень числителя
(поскольку степень числителя 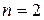 больше степени знаменателя
больше степени знаменателя 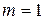 ).
).
Пример 5.6. Найти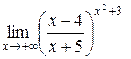 .
.
Неопределённость вида 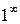 раскроем, используя формулу
раскроем, используя формулу 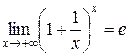 .
.
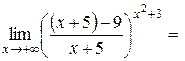
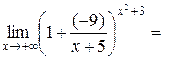
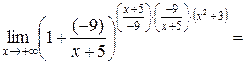
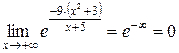 .
.
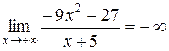 , так как степень числителя больше степени знаменателя (см. п. 1).
, так как степень числителя больше степени знаменателя (см. п. 1).
Пример 5.7. Найти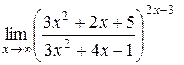 .
.
Выделим целую часть в основании степени:
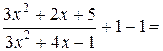
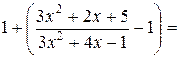
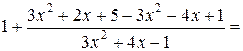
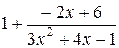 . Тогда
. Тогда 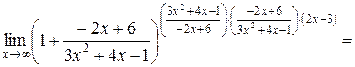
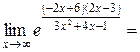
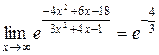 , так как
, так как 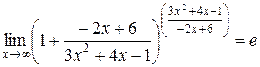 и
и 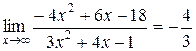 (степень числителя равна степени знаменателя).
(степень числителя равна степени знаменателя).
Пример 5.8. Вычислить 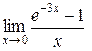 .
.
Имеет место неопределённость вида 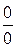 . Воспользуемся таблицей эквивалентных б.м. функций, согласно которой
. Воспользуемся таблицей эквивалентных б.м. функций, согласно которой 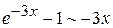 при
при 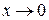 . Тогда
. Тогда 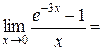
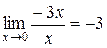 .
.
Пример 5.9. Найти 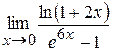 .
.
По таблице эквивалентных б.м. функций 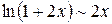 и
и 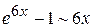 при
при 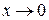 . Следовательно,
. Следовательно,
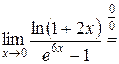
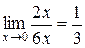 .
.
Пример 5.10. Найти 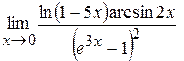 .
.
Воспользуемся таблицей эквивалентных б.м. функций:  ,
, 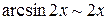 ,
, 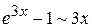 при
при 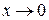 . Тогда
. Тогда
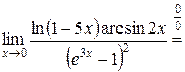
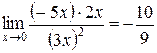 .
.
Пример 5.11. Вычислить 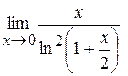 .
.
Имеем 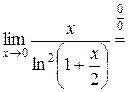
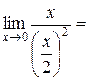
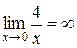 , так как
, так как 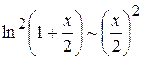 при
при 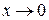 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Первый замечательный предел | | | Точки разрыва функции |
Дата добавления: 2014-02-28; просмотров: 680; Нарушение авторских прав

Мы поможем в написании ваших работ!