
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Расчёт трёхпроводной трёхфазной схемы, когда в линейных проводах включены сопротивления
Когда между генератором и нагрузкой большое расстояние, то необходимо учитывать сопротивления линейных проводов. Линейные провода обладают активным и индуктивным сопротивлениями.
Рассмотрим расчёт схемы соединений треугольник – треугольник (рис. 24).
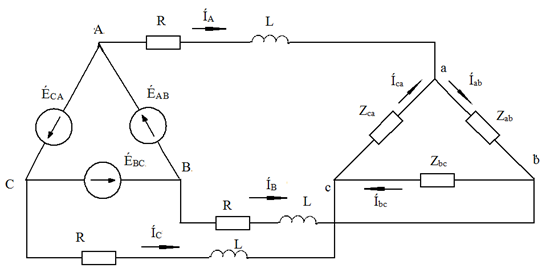
Рис. 24. Схема соединения треугольник - треугольник
Будем считать, что нагрузка неравномерная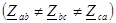 . На схеме рис. 24 обозначено: R – активное сопротивление линейного провода, L – индуктивность линейного провода.
. На схеме рис. 24 обозначено: R – активное сопротивление линейного провода, L – индуктивность линейного провода.
Ни один из выше рассмотренных методов расчёта напрямую не подходит для расчёта данной схемы.
Перед расчётом известны все линейные ЭДС генератора Е́АВ, Е́ВС, Е́СА, комплексные сопротивления нагрузок и линейных проводов.
Расчёт любой трёхфазной цепи начинается с написания систем трёх линейных и трёх фазных напряжений генератора. Предположим, что Е́АВ = 380В. Что бы не ошибиться, желательно строить векторную диаграмму линейных и фазных напряжений.
Вектор Е́АВ направлен по вещественной оси комплексной плоскости (рис. 25)
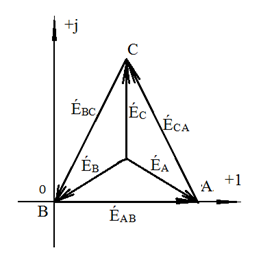
Рис. 25. Векторная диаграмма
 Вектор Е́ВС отстаёт от вектора Е́АВ на 120°. В результате получилась следующая система:
Вектор Е́ВС отстаёт от вектора Е́АВ на 120°. В результате получилась следующая система:
Е́АВ = 380 В
Е́ВС = 380-j120° = -190 – j329,09 В (72)
Е́СА = 380j120° = -190 – j329,09 В
Теперь запишем систему трёх фазных ЭДС генератора. Из векторной диаграммы рис. 25 видно, что ЭДС Е́А отстаёт от Е́АВ на 30°. Треугольник линейных ЭДС равносторонний, все углы по 60°. Фазные ЭДС делят эти углы пополам. Кроме того известно, что фазные ЭДС в 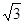 раз меньше линейных:
раз меньше линейных:
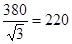
Поэтому для фазной ЭДС генератора можно записать:
Е́А = 220-j30° = 190,526 – j100 В
Фазная ЭДС Е́В отстает от Е́А на 120°:
Е́В = 220-j150° = -190,526 – j100 В
Фазная ЭДС Е́С опережает от Е́А на 120°:
Е́С = 220j90° = j220 В
Запишем теперь систему трёх фазных ЭДС генератора:
 Е́А = 220-j30° = 190,526 – j100 В
Е́А = 220-j30° = 190,526 – j100 В
Е́В = 220-j150° = -190,526 – j100 В (73)
Е́С = 220j90° = j220 В
Пользуемся ли мы системой трёх линейных ЭДС или трёх фазных ЭДС генератора, потенциалы точек А, В, С одинаковый в обоих случаях.
Для расчёта схемы рис. 24 воспользуемся системой трёх фазных ЭДС (73).
Далее следует преобразовать треугольник нагрузок в эквивалентную звезду. Обозначим через Za, Zb, Zc сопротивления эквивалентной звезды. Формулы для расчёта точно такие же, как и на постоянном токе, только расчёт ведётся в комплексных числах. На рис. 26 показана эквивалентная схема.
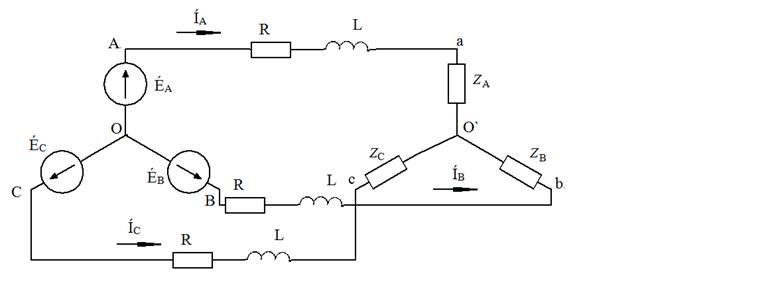
Рис. 26. Эквивалентная схема
Эквивалентные сопротивления звезды рассчитываются по следующим формулам:
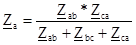 (74)
(74)
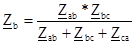 (75)
(75)
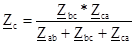 (76)
(76)
В результате от исходной схемы рис. 24 треугольник – треугольник мы перешли к эквивалентной схеме звезда – звезда без нулевого провода, расчёт которой выше рассмотрен. Эта эквивалентная схема нужна, что бы найти линейные токи ÍA, ÍВ, ÍС.
Запишем сначала фазные сопротивления ZА, ZВ, ZС:
ZА = R + jXL + Za; (77)
ZВ = R + jXL + Zb; (78)
ZС = R + jXL + Zc; (79)
Далее найдем напряжение ÚO`O:
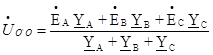 (80)
(80)
А потом найдем линейные токи:
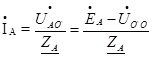 ; (81)
; (81)
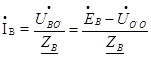 ; (82)
; (82)
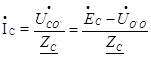 ; (83)
; (83)
Теперь надо вернуться к исходной схеме рис. 24 и найти потенциалы точек a, b, c:
ϕ́а = Е́А – ÍA(R + jXL) (84)
ϕ́b = Е́B – ÍB(R + jXL) (85)
ϕ́c = Е́С – ÍС(R + jXL) (86)
Далее в схеме рис. 24 найдем фазные токи нагрузок
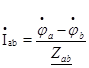 (87)
(87)
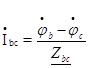 (88)
(88)
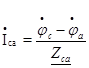 (89)
(89)
Балансы активных и реактивных мощностей и векторную диаграмму следует делать по исходной схеме рис. 24.
Векторная диаграмма начинается с построения системы трёх линейных ЭДС генератора Е́АВ, Е́ВС, Е́СА. Далее следует построить векторы токов, чтобы на диаграмме выполнялись следующие соотношения:
ÍA + ÍB + ÍC = 0; (90)
ÍА = Íаb – Íca; (91)
ÍВ = Íbc – Íab; (92)
ÍС = Íca – Íbc; (93)
Далее следует посчитать падения напряжений на всех элементах схемы и построить их на диаграмме, чтобы выполнялись следующие соотношения
Е́АВ = -ÍBR – ÍBjXL + ÍabZab + ÍAjXL + ÍAR; (94)
Е́CВ = -ÍCR – ÍCjXL + ÍbcZbc + ÍBjXL + ÍBR; (95)
Е́CA = -ÍAR – ÍAjXL + ÍcaZca + ÍCjXL + ÍCR; (96)
Так будет построена полная векторная диаграмма трёхфазной цепи
рис. 24.
| <== предыдущая страница | | | следующая страница ==> |
| Расчёт схемы звезда – звезда без нулевого провода | | | Активная, реактивная и полная мощности трёхфазной системы |
Дата добавления: 2014-02-26; просмотров: 707; Нарушение авторских прав

Мы поможем в написании ваших работ!