Получение кругового вращающегося магнитного поля

Круговое вращающееся магнитное поле представляет собой поле, вектор результирующей магнитной индукции которого по величине неизменен и вращается с постоянной угловой скоростью ω.

Расположим тир одинаковых катушки так, что оси их будут смещены на 120° по отношению друг к другу (рис. 37). Присоединим катушки к симметричной трёхфазной системе ЭДС. Пусть токи входят в начала катушек «н» и изменяется следующим образом:

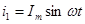
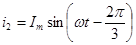(122)

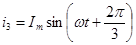
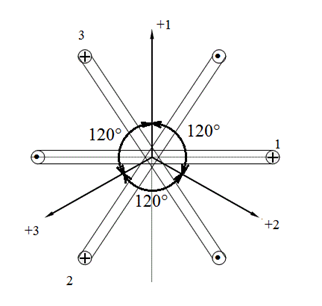
Рис. 37. Взаимное расположение трёх катушек

Графики токов, протекающих по катушкам, показаны на рис. 38.

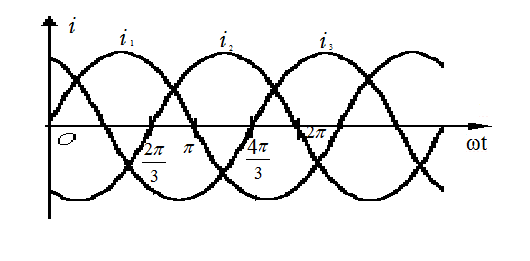
Рис. 38. Графики токов, протекающих в катушке

Каждый из токов будет создавать пульсирующее магнитное поле, направленное вдоль оси своей катушки. Положительное направление оси первой катушки обозначают +1, второй +2, третий +3 (рис. 37).

Поскольку система линейная, так как окружающая среда воздух, то при протекании синусоидальных токов по трём катушкам в них возникают синусоидальные магнитные потоки. Магнитные индукции в катушках так же будут синусоидальными. Магнитную индукцию первой катушки обозначим В₁, второй – В₂, третьей – В₃. Тогда

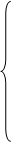
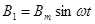
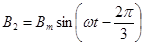(123)

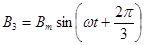
Изобразим векторы 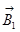,,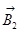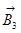и результирующий вектор магнитной индукции 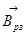для моментов времени ωt = 0, π/2, π, 3π/2. Кроме осей +1, +2, +3 введём декартову систему координат.

На рис. 39 векторы магнитной индукции изображены для ωt = 0.

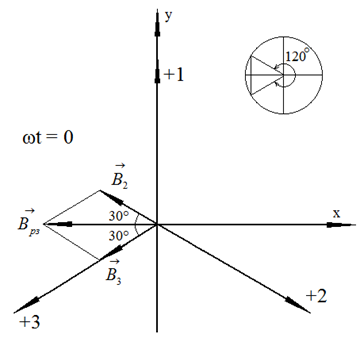
Рис. 39. Расположение векторов магнитной индукции при ωt = 0

Подставим ωt = 0 в выражения (123):

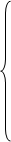
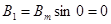
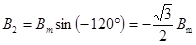(124)

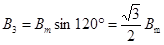
Вектор 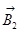направлен в отрицательном направлении оси +2. Вектор 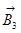направлен в положительном направлении оси +3.

Вектор результирующей магнитной индукции равен векторной сумме 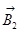и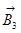

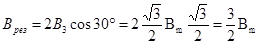
Это получится модуль результирующего вектора магнитной индукции. Из рис. 39 видно, что вектор 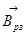направлен в отрицательном направлении оси х. В векторной форме этот вектор равен

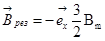(125)

На рис. 40 векторы магнитной индукции изображены для ωt = π/2.

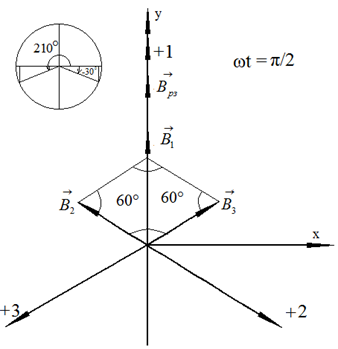
Рис. 40. Расположение векторов магнитной индукции при ωt = π/2

Подставим ωt = π/2 в выражения (123):

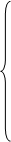
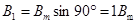
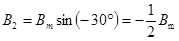(126)

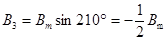
Векторы 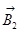и 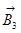направлены в отрицательном направлении осей +2 и +3 соответственно. Вектор 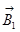направлен в положительном направлении оси +1. Векторное сложение 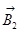и 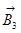даёт вектор, равный , так как в равностороннем треугольнике все углы равны 60°.

Модуль результирующего вектора магнитной индукции

Из рис. 40 видно, что результирующий вектор магнитной индукции 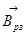направлен в положительном направлении оси y:

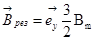(127)

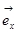где и 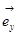- единичные орты по осям х и у.

Таким образом, при изменении ωt на π/2 результирующий вектор магнитной индукции 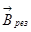так же поворачивается на π/2, оставаясь при этом неизменном по величине.

На рис. 41 векторы магнитной индукции изображены для ωt = π.

Рис. 41. Расположение векторов магнитной индукции при ωt = π

Подставим ωt = π. В выражения (123)

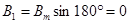
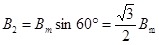(128)

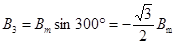
Вектор 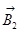направлен в положительном направлении оси +2, вектор 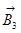направлен в отрицательном направлении оси +3. Модуль результирующего вектора магнитной индукции 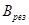равен:

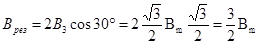
Из рис. 41 видно, что вектор результирующей магнитной индукции направлен в положительном направлении оси х:

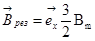(129)

Таким образом, при дальнейшем увеличении ωt на π/2 результирующий вектор магнитной индукции 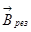опять поворачивается на π/2, оставаясь при этом неизменным по величине.

На рис. 42 векторы магнитной индукции изображены для ωt = 3π/2.

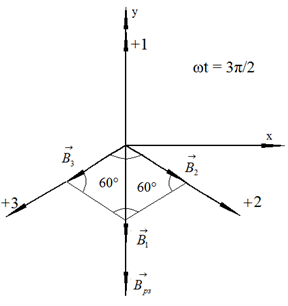
Рис. 42. Расположение векторов магнитной индукции при ωt = 3π/2

Подставим ωt = 3π/2 в выражения (123):

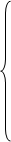
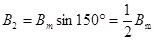(130)

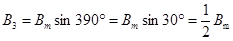
Векторы 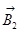и 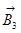направлены в положительном направлении осей +2 и +3 соответственно. Вектор 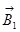направлен в отрицательном направлении оси +1. Векторное сложение 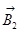и 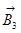даёт суммарный вектор длиной , так как в равностороннем треугольнике все углы по 60°.

Модуль результирующего вектора магнитной индукции равен:

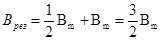
Из рис. 42 видно, что результирующий вектор магнитной индукции направлен в отрицательном направлении оси y:

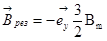(131)

Таким образом, при дальнейшем увеличении ωt на π/2 результирующий вектор магнитной индукции 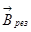опять поворачивается на π/2, оставаясь при этом неизменным по величине.

Дальнейшее увеличение ωt на π/2 приводит к тому, что произошло изменение ωt на 2π, завершился один полный оборот. Расположение векторов магнитной индукции опять стало как на рис. 39.

Таким образом, с увеличением ωt а значит и времени вектор результирующей магнитной индукции, оставаясь по величине равным 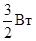, вращается равномерно с угловой скоростью ω в сторону катушки с отстающим током, т. е. от первой ко второй и т. д.

Конец вектора результирующей магнитной индукции 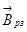описывает окружность. Поэтому говорят, что получается круговое вращающееся магнитное поле.

Если ток 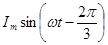пропустить по третьей катушке, а ток 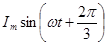- по второй катушке, то направление вращения магнитного поля изменится на противоположное.

Если произойдет обрыв одной из фаз, или токи в катушках будут разными по амплитуде, то вместо кругового вращающегося магнитного поля образуется эллиптической вращающееся магнитное поле. Вектор результирующей магнитной индукции будет скользить по эллипсу.

Вращающееся магнитное поле используется в электродвигателях.

Дата добавления: 2014-02-26; просмотров: 793; Нарушение авторских прав

Мы поможем в написании ваших работ!