
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Ускорение при движении по окружности с постоянной по модулю скоростью
Ускорение равно 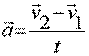 , чтобы найти модуль этого вектора надо вычислить величину
, чтобы найти модуль этого вектора надо вычислить величину 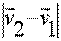
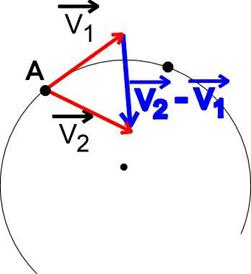
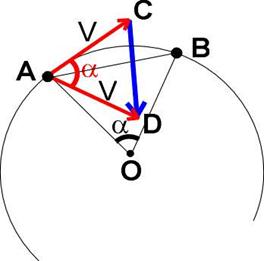
| Рассмотрим движение мат. точки на очень маленьком участке траектории АВ. Точки А и В расположены очень близко друг к другу, но мы их на чертеже разнесли подальше, чтобы лучше разобраться в чертеже. Векторы скорости имеют разное направление, но одинаковую величину. | 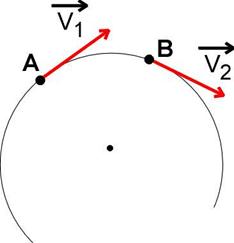
|
Построим вектор изменения скорости 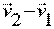 .
Для этого перенесем вектор V2 в точку А. Построим разность векторов .
Для этого перенесем вектор V2 в точку А. Построим разность векторов 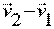 . .
| 
|
Рассмотрим треугольники АОВ и ACD.
1. они оба равнобедренные (АО=ОВ=R и AD=AC=v),
2. АО перпендикулярно АС, ОВ перпендикулярно AD, как радиусы и соответствующие касательные.
3. Углы DAC=AOB=a, так как они образованы взаимно перпендикулярными сторонами.
Следовательно, эти треугольники подобны. Поэтому имеем следующее соотношение:
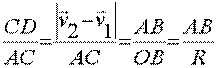 Хорда АВ практически равна дуге АВ, так как точки А и В очень близки друг к другу. Поэтому вместо величины хорды АВ можно подставить величину дуги АВ, которая равна vt. Поэтому имеем:
Хорда АВ практически равна дуге АВ, так как точки А и В очень близки друг к другу. Поэтому вместо величины хорды АВ можно подставить величину дуги АВ, которая равна vt. Поэтому имеем:
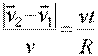 отсюда получаем отсюда получаем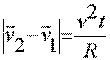 Теперь получаем:
Теперь получаем:
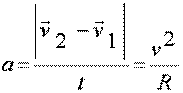
| 
|
| Направлено ускорение к центру окружности, поэтому и называют его центростремительным. | 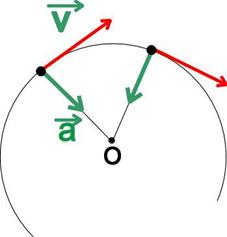
|
| <== предыдущая страница | | | следующая страница ==> |
| Движение тела по окружности с постоянной по модулю скоростью | | | Взаимодействие тел. Принцип суперпозиции сил. Законы динамики Ньютона |
Дата добавления: 2014-02-26; просмотров: 603; Нарушение авторских прав

Мы поможем в написании ваших работ!