Движение точки по окружности

Пусть твердое тело вращается вокруг неподвижной оси. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть радиус окружности, описываемый некоторой точкой R. Ее поворот на некоторый угол Δφ можно задать в виде вектора 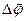. Элементарные углы поворота принято рассматривать, как векторы, направление которых совпадает с направлением движения острия винта, рукоятка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта.

Если за промежуток времени Δt тело поворачивается на угол Δφ, то быстрота его вращения характеризуется угловой скоростью

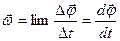(рад/c).

Вектор угловой скорости направлен по оси вращения в сторону, определяемую по правилу правого винта, он представляет собой псевдовектор, как и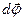

Модуль вектора угловой скорости .

Вращение с постоянной скоростью (ω=const) называется равномерным и , где φ - конечный угол поворота за время t.

Равномерное вращение можно охарактеризовать

1) периодом вращения (обращения) – временем одного полного оборота тела вокруг оси вращения;

2) частотой - числом оборотов в единицу времени.

Так как при Δt=Т Δφ=2π, то 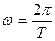и , .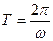

Вектор может изменяться как за счет изменения скорости вращения тела вокруг оси (в этом случае он изменяется по величине), так и за счет поворота оси вращения в пространстве (в этом случае он изменяется по направлению). Пусть за время Δt вектор получаем приращение Δ .

Угловым ускорением называется векторная величина, равная

(Δt→0), 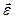- псевдовектор.

При ускоренном движении направление вектора 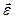совпадает с . При замедленном движении эти вектора направлены противоположно.

Отдельные точки вращающегося тела имеют различные линейные скорости

, т.е. . (1)

За время Δt точка повернулась на Δφ. Точка, находящаяся на расстоянии R от оси вращения проходит путь RΔφ.

Формула (1) связывает линейную и угловую скорости.

В векторном виде , при этом модуль векторного произведения равен , а направление совпадает с направлением поступательного движения правого винта при его вращении от к .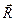

Покажем связь 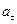и 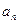с угловыми параметрами.

,

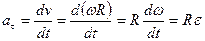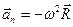(в векторном виде , знак минус, так как вектора 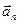и 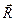противоположно направлены).

Все формулы, связывающие линейные параметры с угловыми параметрами

, , , .

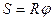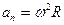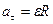В случае равнопеременного движения точки по окружности, т.е. когда ε=const из формул 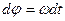и можно получить, что

и , где - начальная угловая скорость.

Дата добавления: 2014-11-08; просмотров: 486; Нарушение авторских прав

Мы поможем в написании ваших работ!