
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Степени свободы и обобщенные координаты
Число независимых координат, полностью определяющих положение точки в пространстве, называют числом степеней свободы. Если точка свободно движется в пространстве, она обладает 3 степенями свободы, если она движется по некоторой поверхности - 2 степенями свободы, если вдоль некоторой линии – 1 степенью свободы.
Все вышесказанное можно обобщить на случай механической системы, состоящей из n материальных точек. Если эти точки могут перемещаться в пространстве без всяких ограничений, то для определения их мгновенного положения надо задать 3n координат.
Не обязательно в качестве независимых координат брать прямоугольные декартовы координаты. Для этой цели могут быть использованы любые f величин: q1, q2,… qf, заданием которых положение материальных точек определяется однозначно. Такие величины называют обобщенными координатами. Производные от обобщенных координат по времени t называют обобщенными скоростями. Так положение материальной точки при ее вращении по окружности можно задать значением центрального угла φ, который радиус-вектор вращающейся точки образует с его положением в некоторый момент времени (например, t=0).
Движение системы определяется полностью, если обобщенные координаты будут найдены как функция времени.
Любое движение твердого тела можно представить как комбинацию поступательного и вращательного движения. Поступательное движение – это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной самой себе.

При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Ось вращения может находиться и вне тела.

Материальная точка при своем движении описывает некоторую линию. Эта линия называется траекторией. В зависимости от формы траектории различают движение прямолинейное, криволинейное, движение по окружности и др.
Сделаем рисунок. Пусть материальная точка движется по криволинейной траектории. В начальный момент времени точка находится в т. А, через некоторое время Δt – в т.В. Длина участка траектории АВ, пройденного материальной точкой за время Δt, называется длиной пути Δs и является скалярной функцией времени ΔS = ΔS(t).
Вектор  , проведенный из начального положения точки в ее конечное положение, называется перемещением точки (вектором перемещения).
, проведенный из начального положения точки в ее конечное положение, называется перемещением точки (вектором перемещения).
|

Скорость – характеристика движения материальной точки, которая определяет быстроту движения и его направление в данный момент времени.
Вектором средней скорости  называют отношение перемещения (приращения
называют отношение перемещения (приращения  радиус-вектора точки) к промежутку времени, в течение которого это перемещение произошло:
радиус-вектора точки) к промежутку времени, в течение которого это перемещение произошло:  =
=  / Δt (см рис.). Направление вектора средней скорости
/ Δt (см рис.). Направление вектора средней скорости  совпадает с направлением вектора перемещения
совпадает с направлением вектора перемещения  .
.
Мгновенной скоростью называют  (Δt→0), т.е. первую производную радиус-вектора по времени.
(Δt→0), т.е. первую производную радиус-вектора по времени.
Вектор скорости, как и любой другой вектор, можно представить в виде  , но
, но  .
.
Из сравнений этих выражений вытекает, что  , т.е. проекции вектора скорости на координатные оси равны производным по времени соответствующей координаты движущейся частицы.
, т.е. проекции вектора скорости на координатные оси равны производным по времени соответствующей координаты движущейся частицы.
Приняв во внимание, что  =
= 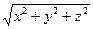 , получим
, получим 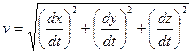 .
.
Модуль мгновенной скорости определяется выражением  , т.е. это первая производная пути по времени. При Δt→0
, т.е. это первая производная пути по времени. При Δt→0  ≈ΔS.
≈ΔS.
Если за сколь угодно малые равные промежутки времени частица проходит по траектории одинаковые расстояния, движение частицы называют равномерным.
При неравномерном движении модуль мгновенной скорости с течением времени меняется. Поэтому для характеристики неравномерного движения используют скалярную величину – среднюю скорость неравномерного движения 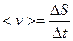 .
.
Длину пути, пройденного точкой за время Δt, можно определить интегрированием уравнения  :
: 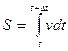 .
.
Скорость движения материальной точки может изменяться как по модулю, так и по направлению. Быстрота изменения скорости по модулю и направлению характеризуется ускорением.
Средним ускорением неравномерного движения называют векторную величину, равную отношению вектора изменения скорости  к интервалу времени Δt, за который это изменение произошло
к интервалу времени Δt, за который это изменение произошло  .
.
Вектор среднего ускорения  совпадает по направлению с вектором изменения скорости
совпадает по направлению с вектором изменения скорости  .
.
Мгновенным ускорением материальной точки в момент времени t называют предел среднего ускорения 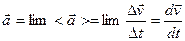 , , т.е. первую производную вектора скорости по времени.
, , т.е. первую производную вектора скорости по времени.
Рассмотрим проекции на координатные оси. С учетом того, что  можно записать
можно записать  .
.
Получаем, что проекция ускорения на ось Х равна второй производной координаты Х по времени. Аналогичные уравнения получаются для проекций ускорения на оси У и Z. Т.о. 
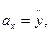
 .
.
Сделаем рисунок. Пусть материальная точка движется по криволинейной траектории. В точке А скорость материальной точки  , в точке В -
, в точке В -  ,
,  . Разложим вектор
. Разложим вектор  на две составляющие.
на две составляющие. 
Для этого из т.А по направлению  отложим вектор
отложим вектор 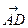 по модулю равный /
по модулю равный /  /. Очевидно, что вектор
/. Очевидно, что вектор  =
= 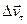 , определяет изменение скорости за время Δt по модулю
, определяет изменение скорости за время Δt по модулю 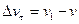 . Вторая составляющая вектора
. Вторая составляющая вектора  - (
- (  ) характеризует изменение скорости за Δt по направлению.
) характеризует изменение скорости за Δt по направлению.
Отсюда вектор полного ускорения тоже можно представить в виде суммы составляющих, одна из которых направлена по касательной к траектории и обозначается 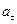 , называется тангенциальным ускорением.
, называется тангенциальным ускорением.
По модулю  , т.е. тангенциальное ускорения есть первая производная по времени от модуля скорости, оно определяет быстроту изменения скорости по модулю.
, т.е. тангенциальное ускорения есть первая производная по времени от модуля скорости, оно определяет быстроту изменения скорости по модулю.
Найдем вторую составляющую ускорения. Будем считать, что т. В достаточно близка к т. А, тогда путь 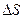 можно считать дугой окружности некоторого радиуса R, т.е.
можно считать дугой окружности некоторого радиуса R, т.е. 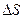 ≈/AB/, мало отличающейся от хорды.
≈/AB/, мало отличающейся от хорды.
Из подобия треугольников АОВ и EAD следует, что
 , но так как
, но так как  и
и 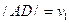 ,
,
то  или
или  .
.
При Δt→0  и
и  .
.
Если Δt→0, угол EAD→0, т.к. ΔEAD равнобедренный, то угол ADE→ 90º, т.е. при Δt→0  перпендикулярен
перпендикулярен  . Так как
. Так как  направлен по касательной к траектории, то
направлен по касательной к траектории, то  ┴
┴  и направлен к центру ее кривизны.
и направлен к центру ее кривизны.
Вторая составляющая ускорения, равная  , называется нормальной составляющей ускорения и направлена по нормали к траектории, к центру ее кривизны, поэтому ее часто называют центростремительным ускорением. Она определяет быстроту изменения скорости по направлению.
, называется нормальной составляющей ускорения и направлена по нормали к траектории, к центру ее кривизны, поэтому ее часто называют центростремительным ускорением. Она определяет быстроту изменения скорости по направлению.
Полное ускорение 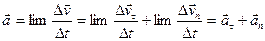 (Δt→0).
(Δt→0).

В зависимости от значений 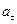 и
и 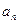 движение можно классифицировать следующим образом:
движение можно классифицировать следующим образом:
1) 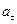 =0,
=0, 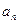 =0 - прямолинейное равномерное движение;
=0 - прямолинейное равномерное движение;
2) 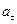 =const,
=const, 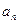 =0 – прямолинейное равнопеременное
=0 – прямолинейное равнопеременное
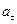 =
=  . Если
. Если  ,
, 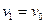 и
и 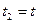 , то
, то 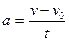 и
и  .
.
Отсюда длина пути  .
.
3) 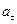 =0,
=0, 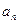 =const – равномерное движение по окружности;
=const – равномерное движение по окружности;
4) 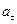 = f (t),
= f (t), 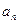 =0 – прямолинейное движение с переменным ускорением;
=0 – прямолинейное движение с переменным ускорением;
5) 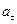 =0,
=0, 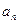 ≠ 0 – равномерное криволинейное;
≠ 0 – равномерное криволинейное;
6) 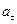 =const,
=const, 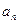 ≠ 0 – криволинейное равнопеременное;
≠ 0 – криволинейное равнопеременное;
7) 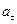 = f (t),
= f (t), 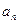 ≠ 0 – криволинейное движение с переменным ускорением.
≠ 0 – криволинейное движение с переменным ускорением.
| <== предыдущая страница | | | следующая страница ==> |
| Движение тел происходит в пространстве и во времени | | | Движение точки по окружности |
Дата добавления: 2014-11-08; просмотров: 481; Нарушение авторских прав

Мы поможем в написании ваших работ!