Движение системы с конечным числом степеней свободы

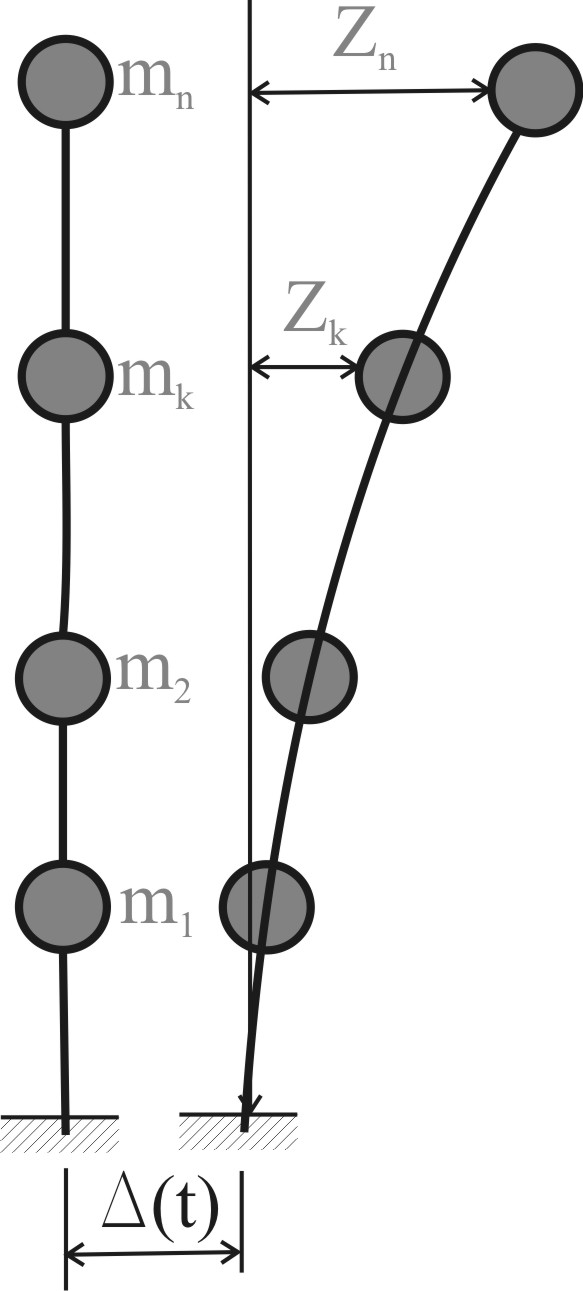Уравнения движения

Разрешающая система уравнений МКЭ – уравнения равновесия узлов.

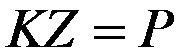
Где 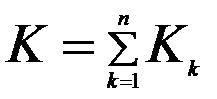– матрица жесткости системы,

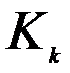– матрица жесткости элементов,

Z – вектор перемещений,

Р – вектор внешних сил.

Решив матричную систему уравнений и найдя Z, вычислим усилия S_k элементов

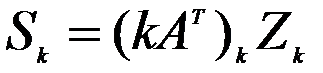
В задачах динамики добавляем по принципу Даламбера силы инерции и диссипативные силы

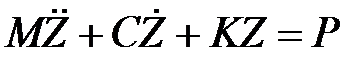
А) Матрица жесткости

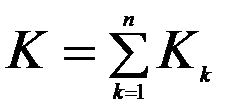,где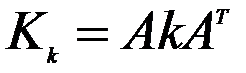

Для стандартных элементов на плоскости

Балочный элемент

Б) Матрица масс конечных элементов

Если заданы точечные массы, то М – диагональная матрица, по соответствующим степеням свободы – эти массы. Если масса распределена – ее можно располагать в узлах. Большее число узлов разбиения приводит к большей точности расчетов. Если погонная масса стержней m,то узловую массу можно собрать собрать так:

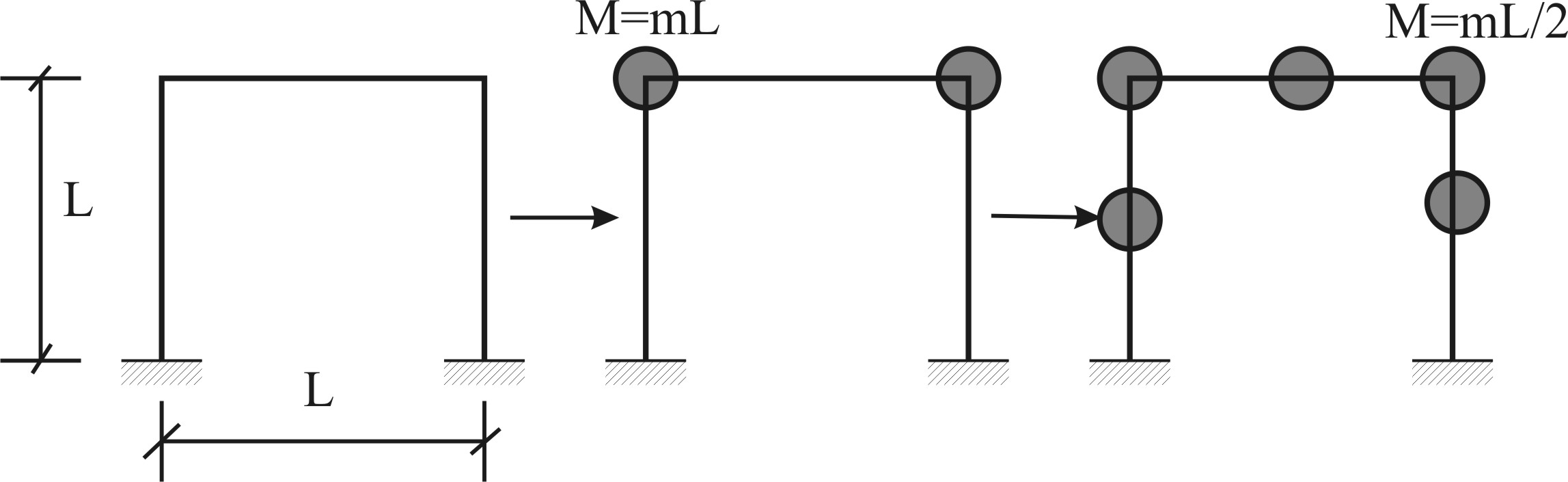
Ниже рассмотрен пример составления матрицы масс. В незаполненных клетках матрицы - нули.

В) Матрица демпфирования

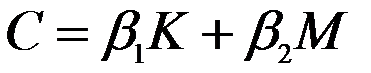
Подробнее учет демпфирования опишем далее.

Свободные колебания

Для чего необходимо изучать свободные колебания?

А) Перед любым сейсмическим расчетом полезно сначала определить спектр частот и формы собственных колебаний, оценить расчетную схему, подобрать соответствующую акселерограмму землетрясений.

Б) Анализ собственных колебаний позволяет получить разрешающие уравнения движения метода модальной суперпозиции, или разложения по собственным формам колебаний.

Итак, при свободных колебаниях С = Р = 0.

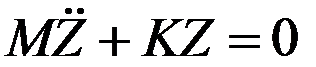
Ищем решение системы, считая колебания гармоническими

,

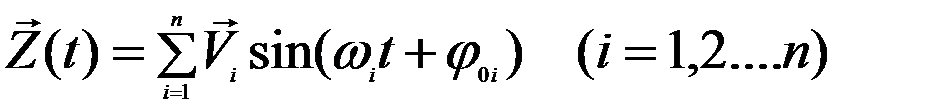Где ω_i , φ_0i – частота и фаза колебаний. Подстановка решения в систему дает

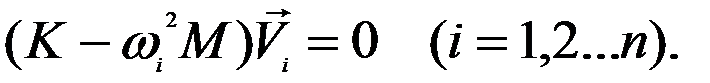(1)

Это система «n» линейных однородных уравнений относительно неизвестных векторов V_i , которые составляют матрицу V:

.

Нетривиальное решение будет, когда определитель

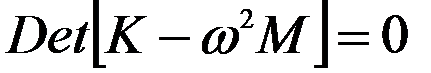
Раскрывая определитель, получаем алгебраическое уравнение n-й степени относительно ω², решение которого дает спектр ω₁, ω₂, … ω_n.

Затем для каждой собственной частоты ω_i из решения системы (n-1) уравнений (1) при, например, заданной величине V_1i = 1определяем формы собственных колебаний

.

Условия ортогональности собственных форм

Рассмотрим i – ю форму колебаний

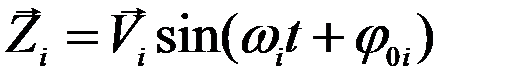
Тогда амплитудное значение вектора перемещений 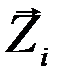и вектора инерционных сил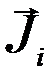

. (2)

Для j –й формы соответственно (стрелки опускаем)

. (3)

Применив теорему Бетти, рассматривая эти состояния как взаимно возможные,

.

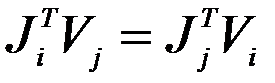Заменяя в последнем выражении инерционные силы по (2) и (3), по правилу транспонирования произведения матриц 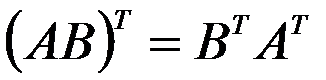получим

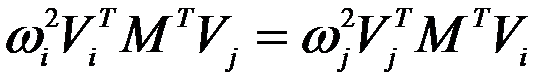. (4)

Зная, что для симметричной матрицы 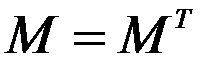, и что 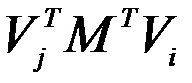- скаляр, значит, выражение для него равно транспонированному, то

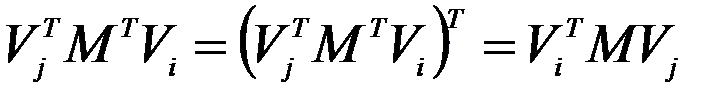, поэтому запишем (4) в виде

.

Т.к. 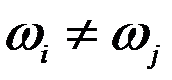, следует .

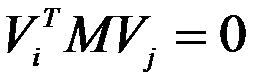Это Первое условие ортогональностисобственных форм колебаний.

Если матрица М диагональная, то .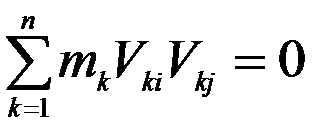

Запишем (1) в виде 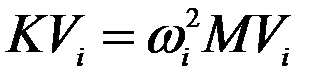и умножим слева на 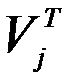, получим

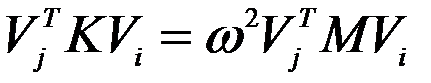т.к. 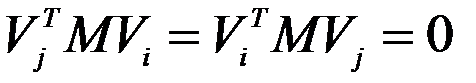, получим

Это Второе условие ортогональностисобственных форм.

Физический смысл полученных условий собственных форм:

1) 1-е условие: Возможная работа внешних сил инерции i – й формы колебаний на перемещениях j – й формы равна нулю.

2) 2 – е условие: Возможная работа внутренних сил упругости i – й формы колебаний на перемещениях j – й формы равна нулю.

Если массы точечные и матрица М диагональна, то первое условие ортогональности можно записать в виде суммы

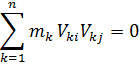
Этим равенством будем проверять расчет на собственные значения – определение частот и форм свободных колебаний конструкций.

Дата добавления: 2014-08-09; просмотров: 734; Нарушение авторских прав

Мы поможем в написании ваших работ!