Определение сейсмических нагрузок для систем со многими степенями свободы. Определение сейсмических нагрузок для систем со многими степенями свободы

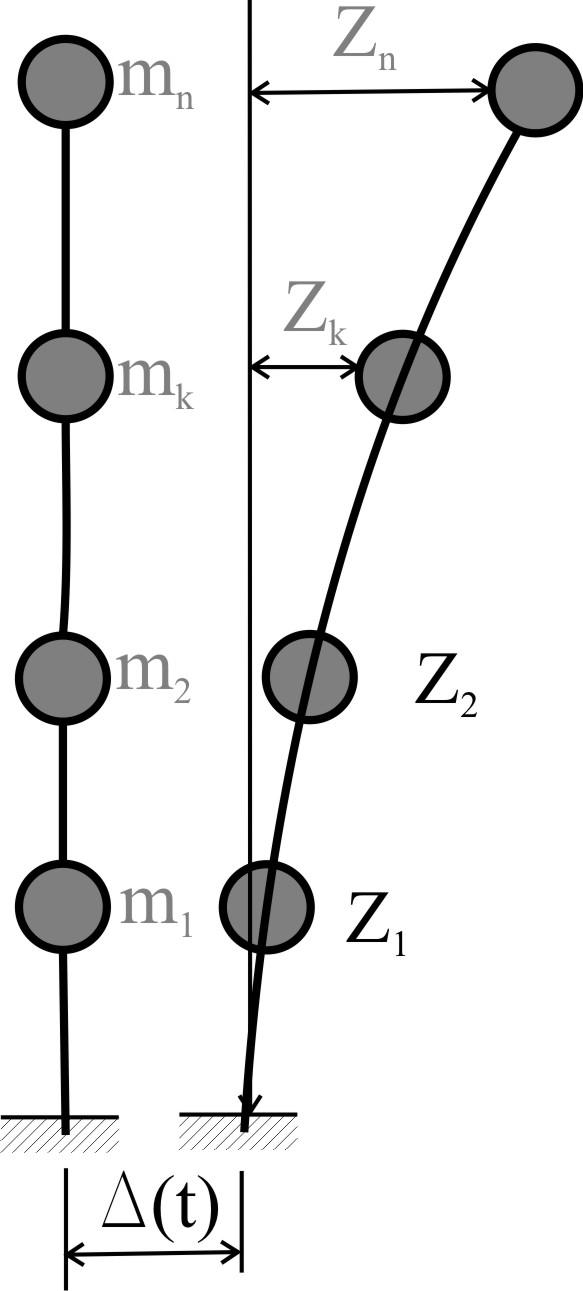Определение сейсмических нагрузок для систем со многими степенями свободы.

(Консольная схема СНиП)

Если 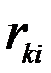- реакция к-й связи от единичного смещения i-й связи (метод перемещений), то уравнения равновесия для к-й массы

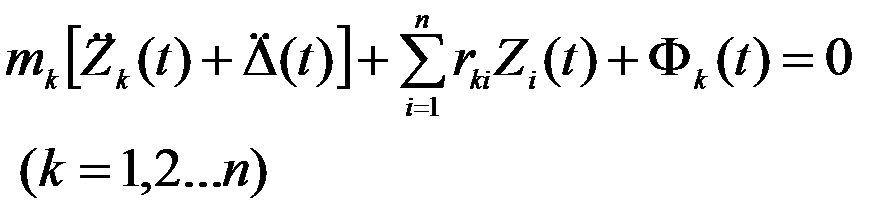(1)

Здесь 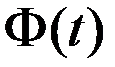- силы сопротивления.

Систему уравнений (1) можно записать в матричной форме

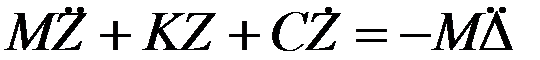. (2)

Здесь 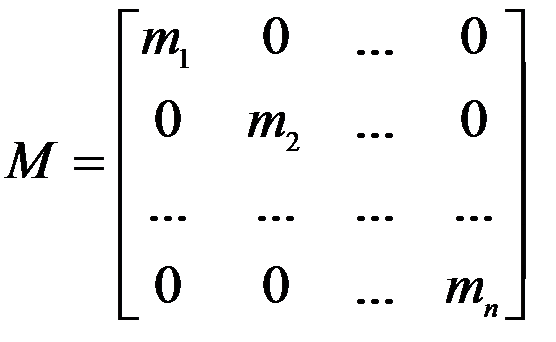Диагональная матрица,

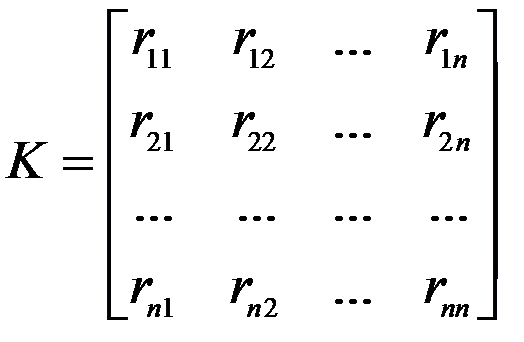Матрица жесткости,

С – матрица демпфирования.

Метод модальной суперпозиции

Задача на собственные значения уже решена, т.е. вычислен спектр частот собственных колебаний и определены их формы. Ищем решение системы (2) в виде суперпозиций форм собственных колебаний

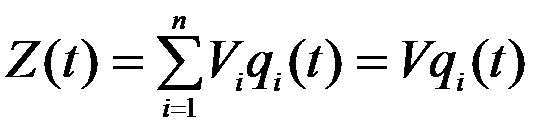, (3)

где 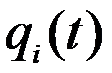- обобщенная координата, соответствующая i-й форме собственных колебаний (функция времени).

Графически это можно представить в виде

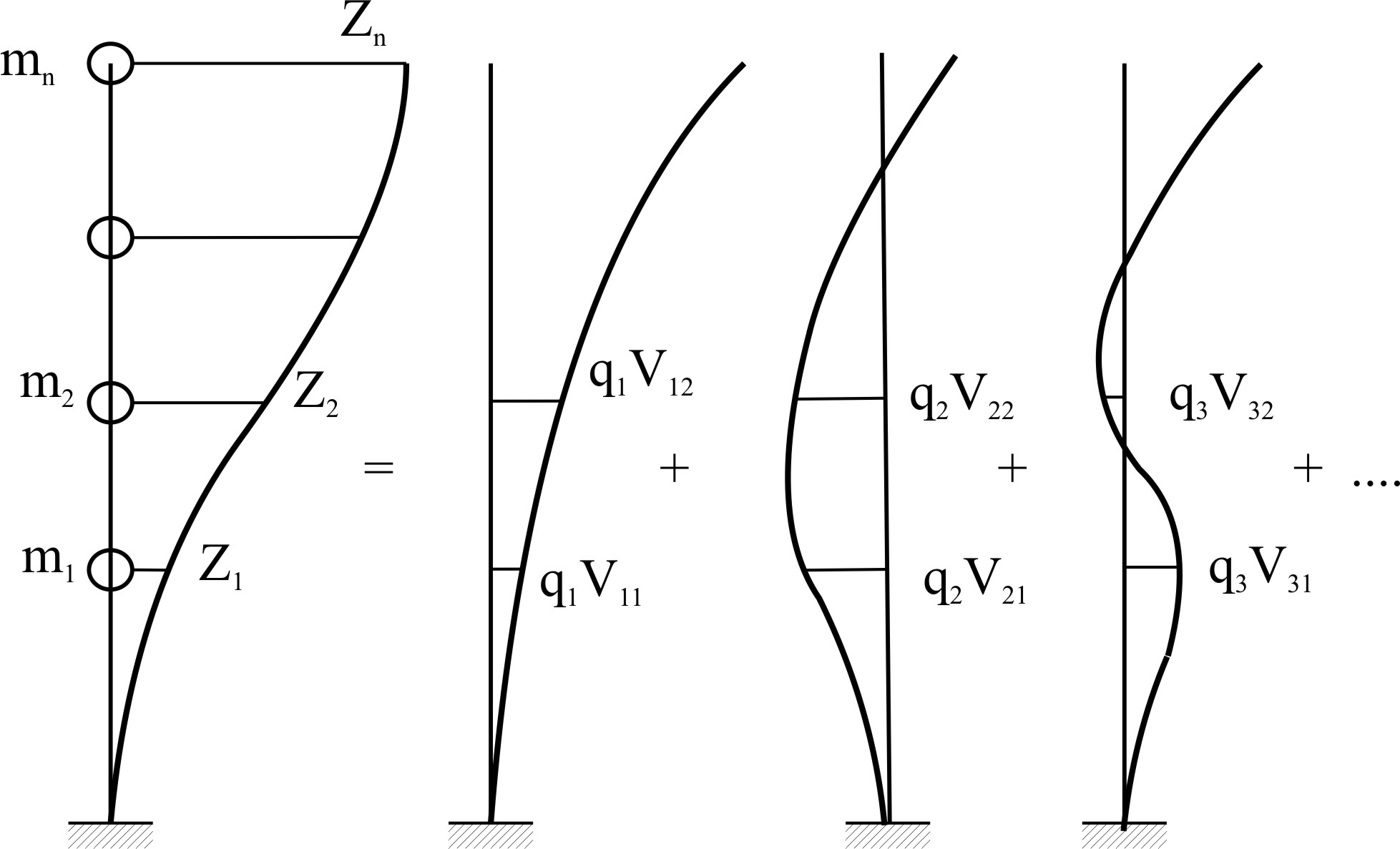
1-я форма 2-я форма 3-я форма

Подставляя (3) в (2) и умножая слева на вектор 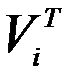получим при Φ = 0

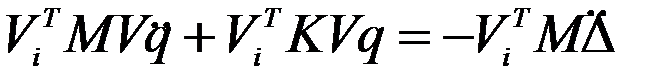(4)

Используя 1 и 2 условия ортогональности

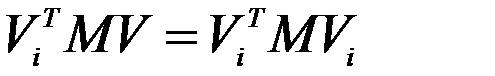и ,

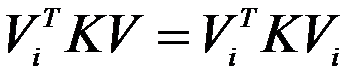Получим

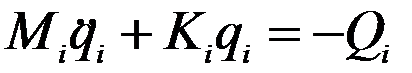, (5)

Где 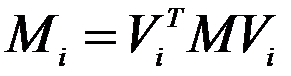- обобщенная масса для i-й формы колебаний (число),

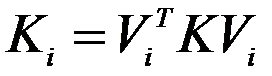- обобщенная жесткость (число),

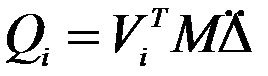- обобщенная нагрузка.

Обобщенную жесткость можно представить

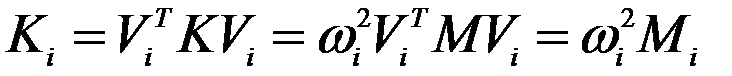(6)

Это равенство следует из формулы (1) предыдущей лекции.

Подставляя (6) в (5) и деля на М_i получим

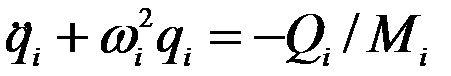(7)

Повторяя процедуру (4-7) для других форм (j) получим другие (n-1) уравнений типа (7). Таким образом, применяя процедуру разложения по собственным формам, мы вместо системы уравнений (2) получили «n» независимых уравнений (7), т.е. система (2) распадается на «n» независимых уравнений, каждое из которых определяет обобщенную координату q_i , отвечающую i – й форме колебаний. Следовательно, решение системы с «n» степенями свободы сводится к решению «n» задач линейного осциллятора.

Учет демпфирования

Отметим, что процедура разделения системы стала возможной потому, что матрица масс и матрица жесткости приводятся к диагональному виду с помощью одного преобразования. Поэтому, для того, чтобы матрица демпфирования также приводилась к диагональному виду, то, вслед за Рэлеем, можно представить ее в виде линейной комбинации этих матриц.

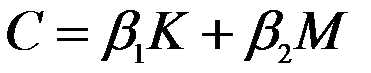
Тогда уравнения движения запишутся так:

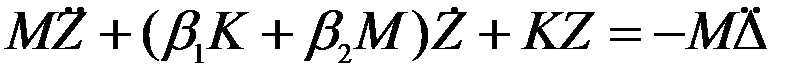
После вышеприведенных преобразований получим

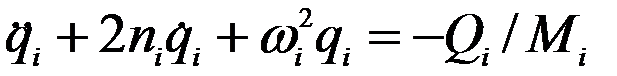
(7-а)

Где 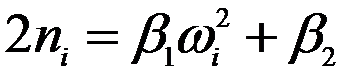- коэффициент затухания.

Получим n_i через коэффициент неупругого сопротивления γ:

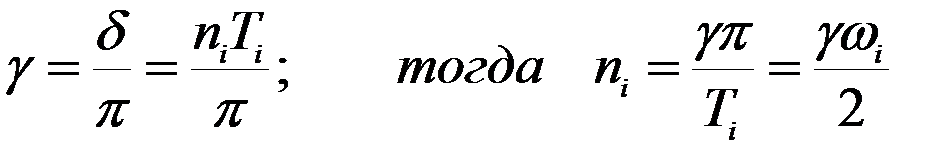
Здесь 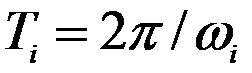период собственных колебаний по i – й форме,

δ – логарифмический декремент колебаний. Можно принять для стальных конструкций γ = 0,01, для железобетонных конструкций γ = 0,01.

Если матрица М диагональна, то

.

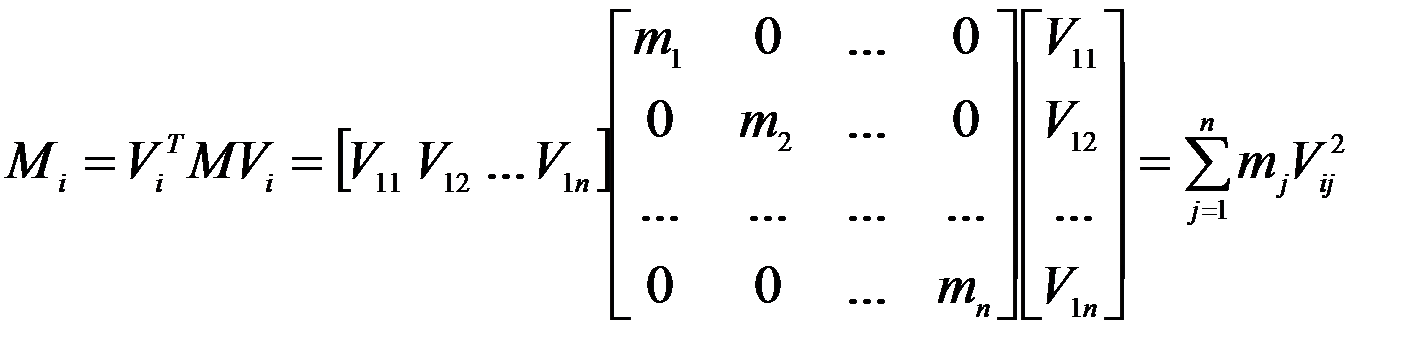Перепишем правую часть уравнения (7-а):

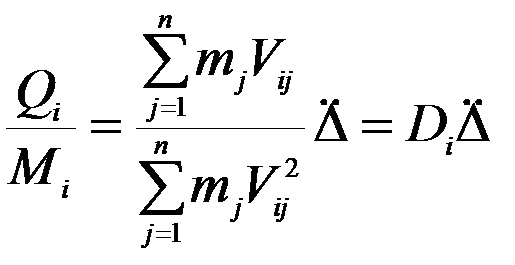(8)

Решение (7-а) через интеграл Дюамеля при нулевых начальных условиях

(9)

Относительное перемещение к-й массы

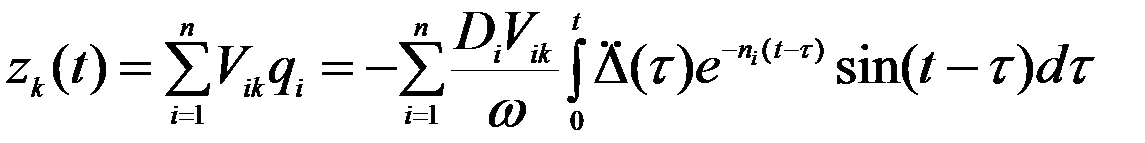
Полное перемещение к-й массы 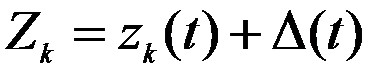, после соответствующих замен

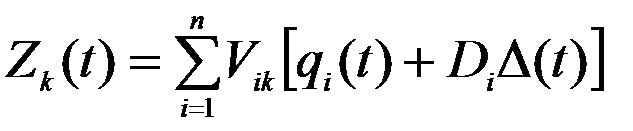
Ускорение к-й массы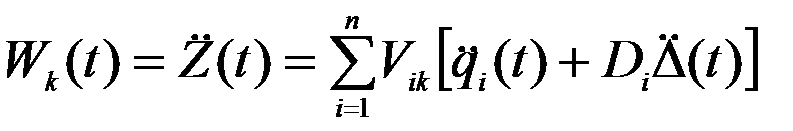

Вычислим инерционную силу, действующую на к-ю массу при колебании по i-й форме

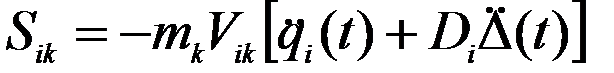(10)

Формула (10) неудобна для пользования из за двойного дифференцирования, поэтому, полагая n«1 (γ«1) получим из (7-а):

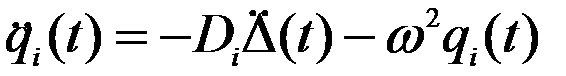(10-а)

Дата добавления: 2014-08-09; просмотров: 433; Нарушение авторских прав

Мы поможем в написании ваших работ!