
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Определение сейсмических сил S при различных законах движения основания
1. Гармонический закон
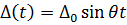
Не учитывая затухание, запишем уравнения движения линейного осциллятора
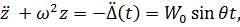 (1)
(1)
Где  - амплитудное значение ускорения.
- амплитудное значение ускорения.
Решение (1) 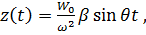
где 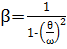 - коэффициент динамичности.
- коэффициент динамичности.
Сейсмическая сила 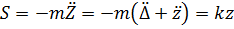 .
.
Напомним, что 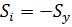 ,
, 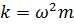 ,
,
поэтому 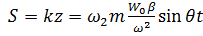 .
. 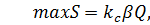
где 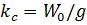 – сейсмический коэффициент, точно совпадает с формулой Мононобе.
– сейсмический коэффициент, точно совпадает с формулой Мононобе.
При учете сил сопротивления коэффициент динамичности
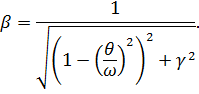
Здесь γ – коэффициент внутреннего неупругого сопротивления. Можно принять приближённо для стальных конструкций γ = 0,01; для железобетонных конструкций γ = 0,1.
Недостатки теории – не учитывает начальных условий и переходных процессов, т.е. сложения вынужденных и свободных колебаний.
Достоинство – внимание к тому, что система сильнее реагирует на ту компоненту колебательного движения, частота которой близка к ее собственной частоте.
2. Учет переходного режима.
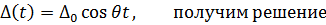
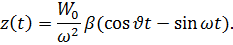
Максимум выражения в скобках = 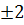 , следовательно, коэффициент динамичности β*2, т.е. увеличивается вдвое. Этот эффект похож на внезапное приложение нагрузки.
, следовательно, коэффициент динамичности β*2, т.е. увеличивается вдвое. Этот эффект похож на внезапное приложение нагрузки.
3. Кратковременный импульс.
Аналогично с помощью интеграла Дюамеля получим выражение для перемещения, а затем и для сейсмической силы для случая действия ускорения по закону прямоугольника.
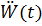
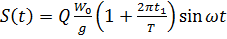
W0
t
t1
Выражение в скобках можно считать β – коэффициент динамичности.
Если считать  поэтому полученная формула похожа на формулу статической теории
поэтому полученная формула похожа на формулу статической теории
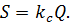
4. Спектральная теория сейсмостойкости.
| Z(t) |
| z(t) |
| D |
| (t) |
m 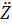 = S = S
|
| сила инерции |
| kz = S |
| y |
| сила упругости |
| m |
| m |
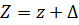
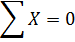
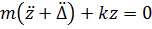
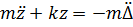
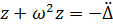
Здесь 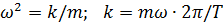
Решение дифференциального уравнения – через интеграл Дюамеля
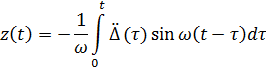
Сейсмическая сила 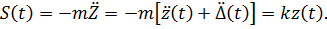
Тогда 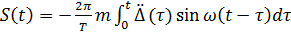
Запишем последнее равенство так:
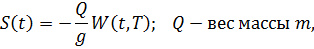
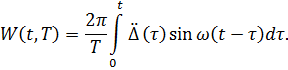
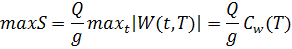
Функция 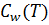 – это максимальное значение функции W(t,T) на рассматриваемом отрезке времени и является функцией T.
– это максимальное значение функции W(t,T) на рассматриваемом отрезке времени и является функцией T.
Для определенного значения γ и при заданной функции 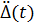 зависимость между
зависимость между 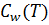 и T можно выразить некоторой кривой, которая называется спектральной кривой ускорений, а сама функция
и T можно выразить некоторой кривой, которая называется спектральной кривой ускорений, а сама функция 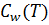 называется спектром ускорений.
называется спектром ускорений.
Аналогично вводятся спектры скоростей 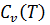 и спектры смещений
и спектры смещений 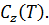 Зависимости:
Зависимости: 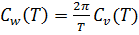 =
= 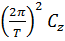 (T) получены в предположении, что зависимость спектра перемещений от времени представляет собой гармоническую функцию. В таком случае спектр максимальных скоростей определяется выражением:
(T) получены в предположении, что зависимость спектра перемещений от времени представляет собой гармоническую функцию. В таком случае спектр максимальных скоростей определяется выражением:
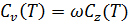 , что следует из правила дифференцирования гармонических функций. Так как полученный таким образом спектр скоростей не является точным, его называют псевдоспектром. Точно так же получается псевдоспектр ускорений:
, что следует из правила дифференцирования гармонических функций. Так как полученный таким образом спектр скоростей не является точным, его называют псевдоспектром. Точно так же получается псевдоспектр ускорений: 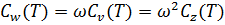 .
.
Задавая различные законы входного воздействия 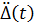 , соответствующие различным землетрясениям, получим семейство спектральных кривых, отличающихся друг от друга (в зависимости от грунтов, магнитуд, расстояний от эпицентра).
, соответствующие различным землетрясениям, получим семейство спектральных кривых, отличающихся друг от друга (в зависимости от грунтов, магнитуд, расстояний от эпицентра).
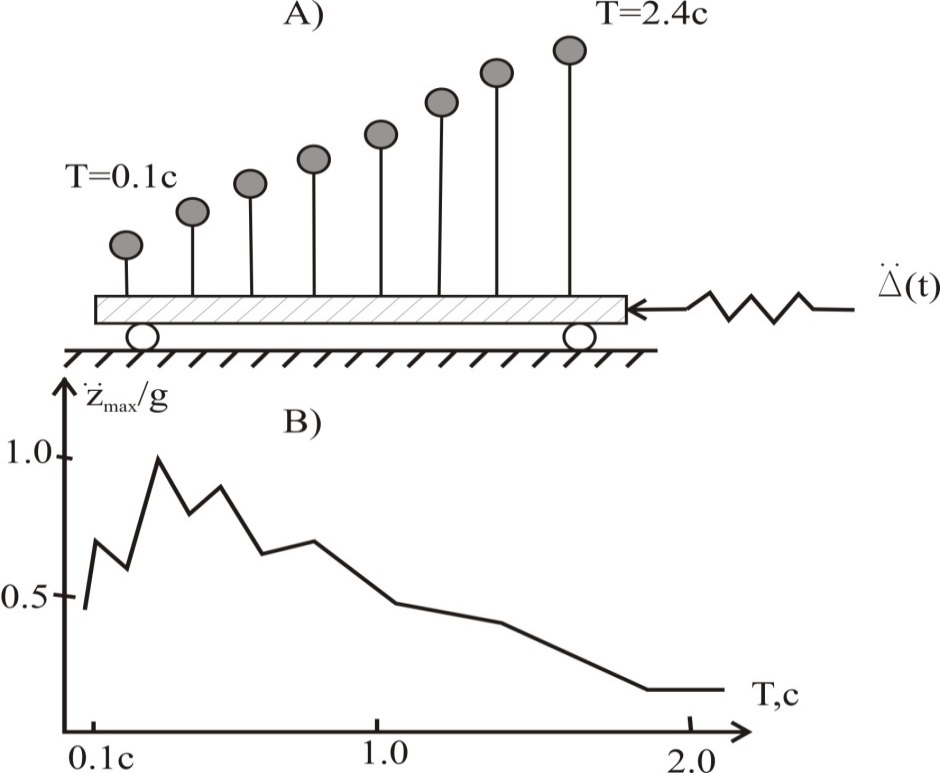
Для получения этих кривых М. Био предложил механическую модель, состоящую из набора маятников, имеющих различные периоды собственных колебаний Т = 0,1 – 2,4с, установленных на подвижной платформе – (рис. А). Этой платформе придавалось движение, соответствующее ускорению колебаний грунта при землетрясении. Маятники моделировали по частотным характеристикам реальные сооружения. Во время опытов фиксируются максимальные величины ускорений 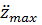 их масс. Строился график (рис В), показывающий зависимость максимальных ускорений масс маятников от их периодов собственных колебаний, т. е. получить спектры этих ускорений. Такие спектры могут быть построены для различных землетрясений.
их масс. Строился график (рис В), показывающий зависимость максимальных ускорений масс маятников от их периодов собственных колебаний, т. е. получить спектры этих ускорений. Такие спектры могут быть построены для различных землетрясений.
Но есть и некоторые общие свойства. При Т = 0,2 – 0,6с наблюдаются пики, которые затем сглаживаются. При Т < 0.2c достоверность данных уменьшается из-за несовершенства приборов. Если провести огибающую всех спектральных кривых, то ее можно принять в качестве расчетной кривой, определяющей возможные максимальные значения инерционных сил линейного осциллятора.
При современных средствах вычислительной техники можно получить спектр ускорений по следующему алгоритму:
1. Моделируем на компьютере систему с 1 степенью свободы, например, невесомый стержень с массой на конце, задаем акселерограмму, решаем задачу и находим максимальное перемещение.
2. Повторяем решение с другой массой, т.е. с другим периодом собственных колебаний, и таких решений должно быть 50 – 100, на всем интервале расчетных периодов, т.е. получаем спектр перемещений Cz.
3. Строим псевдоспектр ускорений по формуле 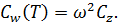
Нормативный метод расчета линейного осциллятора на сейсмическое воздействие
В нормах СССР в основу расчета был положен спектр ускорений в виде:
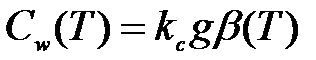 ,
,
где kc – коэффициент сейсмичности, зависящий от балльности района строительства, а β(T) – коэффициент динамичности, зависит от периода собственных колебаний системы.
Для системы с 1 степенью свободы формула для определения сейсмической нагрузки S
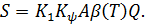
Необходимо уметь объяснить каждый коэффициент формулы СНиП:
Здесь А = 0,1; 0,2; 0,4 для районов с расчетной сейсмичностью 7, 8, 9 баллов.
Этот коэффициент определяет максимальное ускорение в долях от ускорения свободного падения:
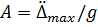
Для 7 баллов 
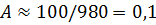 ,
,
Для 8 баллов 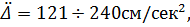
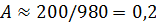 ,
,
Для 9 баллов 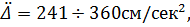
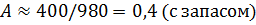 .
.
K1 зависит от степени допускаемых повреждений зданий, принимается по таблице 3* СНиП II-7-81* от 0,12 для сооружений, где могут быть допущены значительные остаточные деформации или локальные повреждения до 1,0, где не допускаются повреждения.
Кψ коэффициент, зависящий от характера деформативности здания, принимается по таблице 6* СНиП II-7-81* от1 до 1,5.
Q – вес массы m.
β(T) – коэффициент динамичности, определяющий характер спектральной кривой.
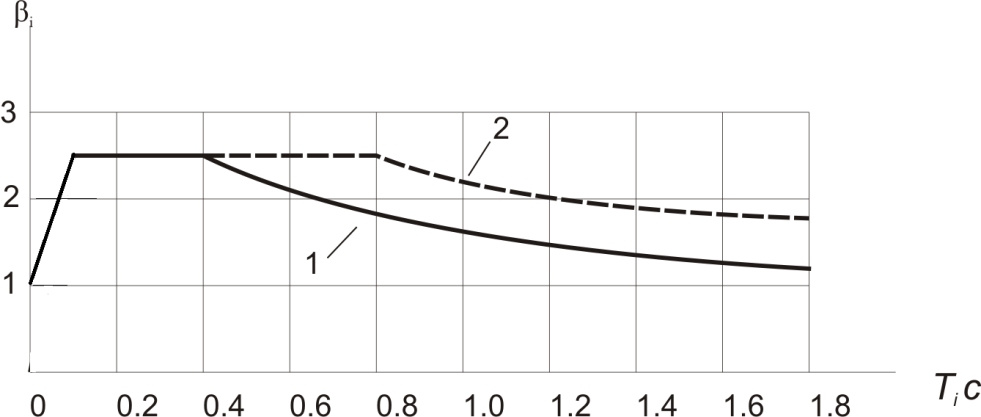
Описание категорий грунтов по сейсмическим свойствам приводится в таблице 1* СНиП II-7-81*. Аналитическое описание этих кривых дается через значения коэффициента динамичности 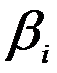 в зависимости от расчетного периода собственных колебаний
в зависимости от расчетного периода собственных колебаний 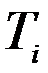 здания или сооружения по
здания или сооружения по 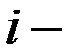 му тону.
му тону.
Для грунтов I и II категорий по сейсмическим свойствам (кривая 1)
 при
при 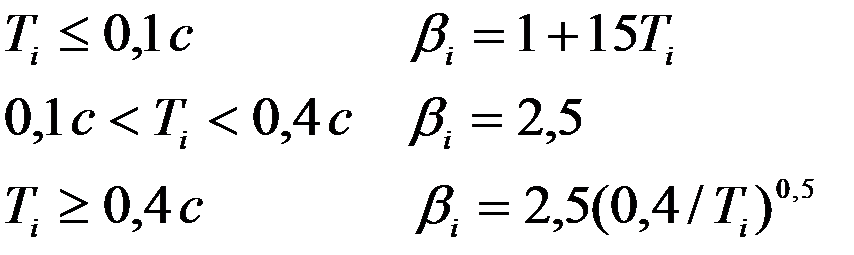
Для грунтов III категории по сейсмическим свойствам (кривая 2).
при 
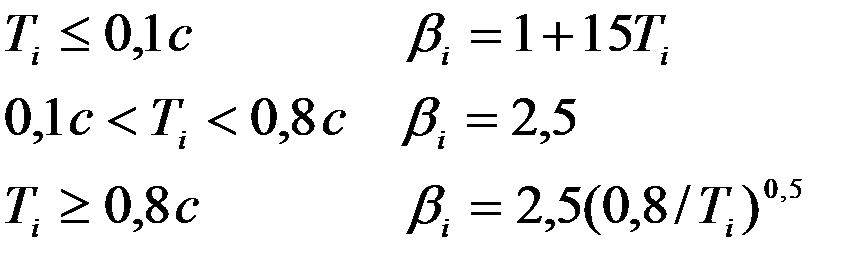
Во всех случаях значения 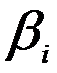 должны приниматься не менее 0,8.
должны приниматься не менее 0,8.
| <== предыдущая страница | | | следующая страница ==> |
| Развитие теории сейсмостойкости | | | Движение системы с конечным числом степеней свободы |
Дата добавления: 2014-08-09; просмотров: 831; Нарушение авторских прав

Мы поможем в написании ваших работ!