
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Развитие теории сейсмостойкости
После разрушительного землетрясения в Японии в 1906 г. Омори провел серию экспериментов по определению сейсмических сил в кирпичных столбиках, расположенных на платформе, перемещающейся горизонтально по гармоническому закону. Столбики доводилась до разрушения, при этом фиксировались наибольшие ускорения и определялись соответствующие инерционные силы. При этом столбики считались недеформируемыми, поэтому ускорение любой точки столбика принималось равным ускорению основания.
1. Эти исследования положены в основу с т а т и ч е с к о й теории сейсмостойкости. Согласно этой теории значение сейсмических сил определяется выражением:
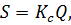
Где 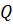 – вес части сооружения, Kc - сейсмический коэффициент, равный отношению ускорения основания к ускорению свободного падения.
– вес части сооружения, Kc - сейсмический коэффициент, равный отношению ускорения основания к ускорению свободного падения.
В этой теории величина сейсмического коэффициента принималась на основе данных о предыдущих землетрясениях, определяющих балльность района. Статическая теория сыграла большую роль в развитии теории сейсмостойкости, впервые предложив количественную оценку сейсмических сил, вызывающих разрушение сооружения.
Однако предположение о недеформируемости сооружения при колебаниях ограничивает область применения этой теории лишь достаточно жесткими сооружениями.
2. Учет деформируемости сооружения привел к созданию д и н а м и ч е с к о й теории сейсмостойкости, описывающей поведение конструкций с помощью методов динамики сооружений. Главной трудностью при этом был недостаток информации о законе движения грунта основания.
Первой попыткой решения задачи о движении системы с одной степенью свободы была работа Мононобе и Сато 1920 г. Движение основания принято синусоидальным, рассматривался процесс стационарных гармонических колебаний консервативной системы с одной степенью свободы. В результате получено решение в виде
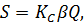
Где β – коэффициент динамичности, определяемый выражением
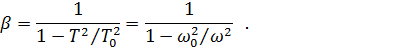
Здесь T(ω) – период (частота) собственных колебаний системы, Т0(ω0) - период (частота) колебания основания при землетрясении.
Затем в 1927 г. Завриев принял косиносуидальный закон движения основания, что позволило учесть внезапность действия сейсмической нагрузки.
3. Развитием теории динамической теории сейсмостойкости явилась с п е к т р а л ь н а я теория, в которой вводятся спектральные кривые, описывающие зависимость максимальных ускорений, скоростей или перемещений линейного осциллятора от периода его собственных колебаний.
Идея спектрального метода определения сейсмических сил впервые предложена Био в 1933 г. Далее метод разрабатывали многие ученые как в СССР, так и за рубежом. Основные положения спектральной теории лежат в методике СНиП, которую подробно рассмотрим дальше.
Расчетная схема сооружений
При сейсмических расчетах расчетная схема сооружений не отличается от аналогичных схем при динамических расчетах, кроме того, что в соответствии со СНиП II-7-81* расчетная схема предписывается в виде консольного стержня с сосредоточенными массами.
Такая схема для многих зданий и сооружений может применяться, например, для каркасных зданий, тогда консоли задают жесткость, равную суммарной жесткости всех стоек, а перекрытия считают жесткими в своей плоскости и абсолютно гибкими из плоскости.
Далее мы рассмотрим методику расчета конструкций, в которой ограничения консольной схемы сняты – можно рассчитывать конструкции произвольного очертания, в том числе и пространственные.
Линейный осциллятор
(Повтор основ динамики)
Рассмотрим вначале действие мгновенного импульса
P
S – импульс 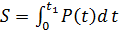
При 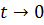 (мгновенный импульс)
(мгновенный импульс)
t
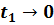
По теореме о сохранении количества движения:
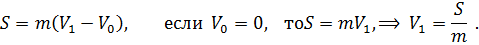
После окончания действия импульса будут свободные колебания
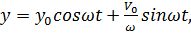 ***
***
| P(t) |
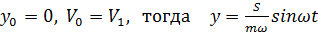
Интеграл Дюамеля
P(τ)
dS
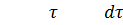
t
y
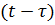
Представим P(t) как последовательность мгновенных импульсов
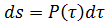 .
.
Каждый импульс ds вызывает согласно *** перемещение
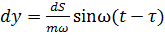
Суммируя влияние всех элементарных импульсов за время t , находим
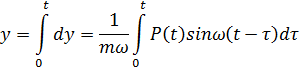
Это интеграл Дюамеля.
Пример.Внезапно приложенная нагрузка.
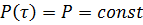
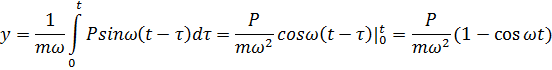
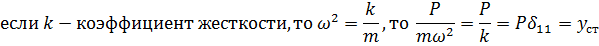
Следовательно 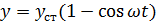 . При
. При 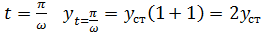
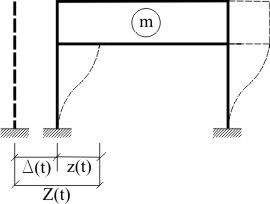
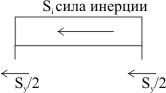
Линейный осциллятор при сейсмическом воздействии
Вывод уравнений движения
Модель
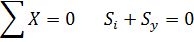
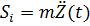
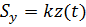 так как
так как 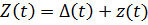 то, опуская далее (t)
то, опуская далее (t)
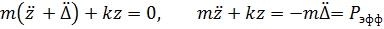
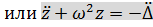
где 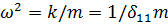 .
.
Решение – с помощью интеграла Дюамеля 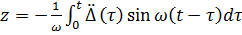
| <== предыдущая страница | | | следующая страница ==> |
| Сейсмические волны | | | Определение сейсмических сил S при различных законах движения основания |
Дата добавления: 2014-08-09; просмотров: 769; Нарушение авторских прав

Мы поможем в написании ваших работ!