
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Звездой
|
Читайте также: |
Соединение трехфазной обмотки трансформатора
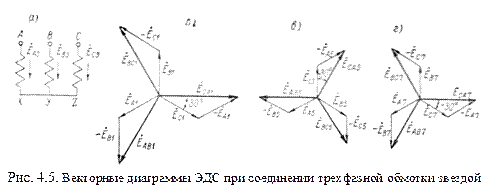
При соединении трехфазной обмотки звездой соединяют в одну общую нейтральную точку либо три начала ее, оставляя свободными концы, либо три ее конца, оставляя свободными начала (рис. 4.5, а). Обходя любой из трех контуров, образуемых звездой, например контур (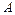 –
– 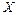 ) – (
) – (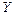 –
–  ), мы идем по обмотке
), мы идем по обмотке 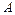 от ее начала
от ее начала 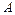 к концу
к концу 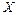 , а по обмотке
, а по обмотке  – от ее конца
– от ее конца 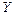 к началу
к началу  , т. е. изменяем направление обхода обмотки В относительно обмотки
, т. е. изменяем направление обхода обмотки В относительно обмотки 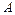 . В этом случае для мгновенных значений линейных имеем:
. В этом случае для мгновенных значений линейных имеем:
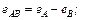 (4.4а)
(4.4а)
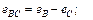 (4.4б)
(4.4б)
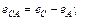 (4.4в)
(4.4в)
Подставляя в эти равенства написанные выше выражения для еА, еB и еC, получаем:
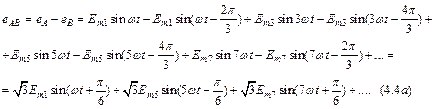
Соответственно
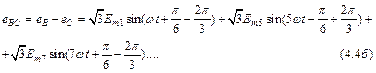
и
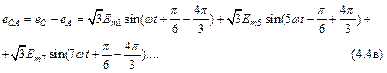
Из уравнений (4.4а), (4.4б) и (4.4в) следует, что при соединении обмоток звездой:
1)гармонические, кратные, трем, в линейном напряжении исчезают; физически это объясняется тем, что по каждому из двух контуров, составляющих звезду, эти гармонические действуют взаимно встречно (рис. 4.5, а);
2)линейные напряжения всех гармонических порядка 3с+ 1, включая сюда и основную, т. е. первую гармоническую, представляют собой симметричные трехфазные системы напряжений с прямым следованием фаз и начальной фазой 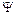
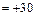 ° (рис. 4.5, б и 4.5, г) и соответственно напряжения всех гармонических порядка 3с-1 -симметричные трехфазные системы с обратным порядком следования фаз и начальной фазой
° (рис. 4.5, б и 4.5, г) и соответственно напряжения всех гармонических порядка 3с-1 -симметричные трехфазные системы с обратным порядком следования фаз и начальной фазой 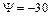 ° (рис. 4.5, в);
° (рис. 4.5, в);
3)амплитуда линейного напряжения любой гармонической порядка 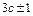 в
в 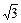 раз больше амплитуды фазного напряжения соответствующей гармонической, т. е.
раз больше амплитуды фазного напряжения соответствующей гармонической, т. е.

где 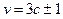 -порядок гармонической.
-порядок гармонической.
Переходя к действующим значениям фазных и линейных ЭДС, имеем:
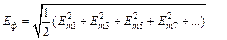 (4.6)
(4.6)
и
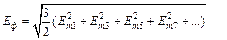 (4.7)
(4.7)
Отсюда следует, что
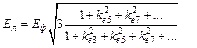 (4.8)
(4.8)
где
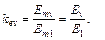 (4.9)
(4.9)
Так как при соединении обмоток звездой фазные токи непосредственно выводятся в линию, то
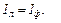 (4.10)
(4.10)
Как известно из курса «Теоретические основы электротехники», при несинусоидальных и токах мощность системы равна сумме мощностей отдельных гармонических. Обычно наибольшее значение имеет мощность первой, или основной, гармонической. Для этой гармонической имеем:
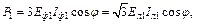 (4.11)
(4.11)
где 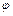 – угол сдвига между
– угол сдвига между 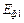 и током
и током 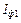 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Трехфазных обмоток трансформатора | | | Треугольником |
Дата добавления: 2014-03-11; просмотров: 542; Нарушение авторских прав

Мы поможем в написании ваших работ!